고전역학 5. 비관성 좌표계

Analytical mechanics/Fowles, Grant R. (7판)의 내용입니다.

가속계

관성계에 대해 병진 가속하는 좌표계를 가속계라고 한다. 기준계의 가속도와 크기는 같고 방향은 반대인 관성력을 물체가 받는 힘에 추가한다. 관성력은 \(F_{i}=-m A_{0}\)와 같다.

[!tip] 사실 중력 = 관성력이다.{title} 아인슈타인은 사고실험을 통해 중력 = 관성력임을 유추해냈다. 따라서, 지구에서 관성력과 같은 다른 가상의 힘을 받으면 관성력 + 중력을 합하여 새로운 중력가속도를 유도해내 사용할 수 있다. ex) 단진자의 주기 \(T=2\pi \sqrt{ \frac{l}{g} }\)에서 새로운 중력가속도 \(\mathbf{g}'\)의 크기를 기존 중력가속도 대신 사용할 수 있다.

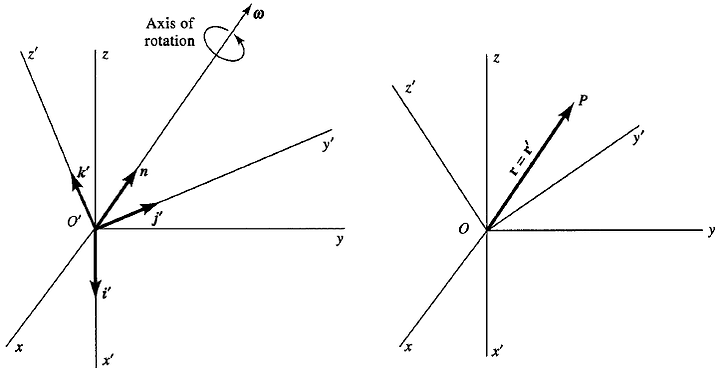
회전계

회전계는 관성계와 원점은 같되 임의의 방향 \(\mathbf{n}\) 방향으로 \(\mathbf{\omega}\) 각속도만큼 회전하는 계로 정의한다. 결론적으로, 비관성 좌표계 내부에서 분석할 때는 관성력 추가하듯 코리올리 가속도, 구심 가속도, 가로 가속도를 추가해주면 관성좌표계 처럼 해석할 수 있다.

• \(\mathbf{a}=\mathbf{a}'+\mathbf{\dot{\omega}} \times \mathbf{r}' + 2 \mathbf{\omega} \times \mathbf{v}' + \mathbf{\omega} \times (\mathbf{\omega} \times \mathbf{r}')\)
  • \(\mathbf{a'}\) : 회전 좌표게에서 볼 때, 물체의 가속도가 있을 때 존재한다.
  • 코리올리 가속도 (Coriolis acceleration) : \(2\omega \times v'\)
    • `코리올리 가속도는, 회전 좌표계에서 볼 때 물체가 움직여야만 존재한다.
  • 구심 가속도 (Centripetal aceleration) : \(\omega \times (\omega \times r')\)
    • 구심 가속도는, 좌표계가 회전할 때 존재한다.
  • 가로 가속도 (transverse acceleration) : \(\dot{\omega} \times r'\)
    • 가로 가속도는, 좌표계의 회전이 가속될 때만 존재한다.
  • \(r', v', a'\)는 회전하는 비관성 좌표계의 관측자가 측정하는 변위, 속도, 가속도이다.
  • 예를들어서, 지구에서 운동하는 물체를 분석하기 위해서 위 힘을 도입한다고 하자. 이 때 r', v', a'는 지구에서 재는 물체의 변위, 속도, 가속도이고, w는 지구의 각속도와 같다.

[!note]- 운동 미분방정식 세우는 방법{title}

\(\mathbf{F}=m \mathbf{a}\) 이고, 관성 좌표계의 가속도와 비관성좌표계의 가속도가 연관된 방정식은

\(\mathbf{a}=\mathbf{a}'+\mathbf{\dot{\omega}} \times \mathbf{r}' + 2 \mathbf{\omega} \times \mathbf{v}' + \mathbf{\omega} \times (\mathbf{\omega} \times \mathbf{r}') + \mathbf{A_{0}}\) 이므로, 비관성 좌표계에서의 운동 방정식은 다음과 같이 쓸 수 있다.

\[\mathbf{F} - m\mathbf{\dot{\omega}} \times \mathbf{r}' - 2 m\mathbf{\omega} \times \mathbf{v}' -m \mathbf{\omega} \times (\mathbf{\omega} \times \mathbf{r}') -m \mathbf{A_{0}} = m \mathbf{a}'\]

두번째 항 = 가로 힘, 세번째 항 = 코리올리 힘, 네번째 항 = 원심력, 다섯번째 항 = 관성력

[!tip] 관성계에서의 벡터와 회전계에서의 벡터가 연관된 방정식을 미분하는 방법{title} 고정계에서 시간으로 미분하는 것은, 회전계에서 시간미분과 \(\mathbf{\omega} \times\)를 더하는 것과 동등하다.

\[\left( \frac{d\mathbf{Q}}{dt} \right)_{fixed}= \left( \frac{d\mathbf{Q}}{dt} \right)_{rot}+ \mathbf{\omega} \times \mathbf{Q} = \left( \frac{d\mathbf{Q}}{dt} \right)_{fixed}= \left[ \left( \frac{d}{dt} \right)_{rot}+ \mathbf{\omega} \times \right] \mathbf{Q}\]

[!tip]- 코리올리, 구심, 가로 가속도가 생각이 안난다면…{title}

\(\mathbf{v}=\mathbf{v'}+ \mathbf{\omega} \times \mathbf{r'}\)에서 양변을 t로 미분해주면 된다.

\[\mathbf{a}=\left[ \frac{d}{dt} + \mathbf{\omega} \times \right]( \mathbf{v'} + \mathbf{\omega} \times \mathbf{r'} )\] \[\mathbf{a}= \frac{d\mathbf{v'}}{dt}+\frac{d}{dt}(\mathbf{\omega} \times \mathbf{r'}) + \mathbf{\omega} \times \mathbf{v'}+ \mathbf{\omega} \times (\mathbf{\omega} \times \mathbf{r'})\] \[\mathbf{a}= \mathbf{a'}+ \mathbf{\dot{\omega}} \times \mathbf{r'} + 2\mathbf{\omega} \times \mathbf{v'}+ \mathbf{\omega} \times (\mathbf{\omega} \times \mathbf{r'})\]

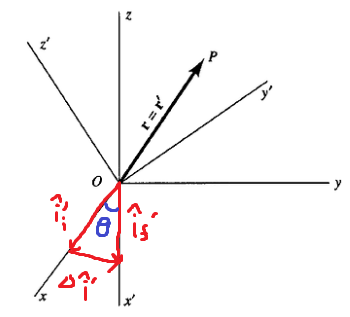
[!note]- 회전계의 basis를 시간에 대해서 미분한 결과{title}

\[\Delta \hat{i}' \simeq \hat{i}' \Delta \theta\] \[d \hat{i}' = \hat{i}' d \theta\] \[\frac{d\hat{i}'}{dt} = \hat{i}' \frac{d\theta}{dt}\] \[\frac{d\hat{i}'}{dt} = \hat{i}' \times \mathbf{\omega}\]

벡터 x 벡터의 결과가 벡터가 나와야 하므로 크로스곱 사용

비관성 좌표계에서 운동분석 하는 방법

운동분석을 하기 위한 좌표계가 가속운동 하고있을 때 비관성 좌표계라고 한다. 비관성 좌표계에서는, 물체에 가상의 힘 몇가지를 추가하면 관성 좌표계처럼 분석할 수 있다.

기준계가 관성계에 대해 병진 + 회전운동 할 때

관성력 + 코리올리힘 + 원심력 + 가로 힘 모두 받고있다고 생각하고 분석하면 된다.

• \(\mathbf{a}= \mathbf{a'}+ \mathbf{\dot{\omega}} \times \mathbf{r'} + 2\mathbf{\omega} \times \mathbf{v'}+ \mathbf{\omega} \times (\mathbf{\omega} \times \mathbf{r'}) + A_{0}\)
  • \(\mathbf{a}\) : 관성 좌표계에서 봤을 때 물체의 가속도
  • \(\mathbf{a'}\) : 회전 + 병진하는 좌표계에서 봤을 때 물체의 가속도
  • \(\mathbf{A_{0}}\) : 병진하는 좌표계에서 느껴지는 가상의 힘 (관성력)
    • \(\mathbf{A_{0}}\)는 좌표계의 가속도와 크기는 같고 방향은 반대이다.
  • 나머지 : 회전하는 좌표계에서 느껴지는 가상의 힘

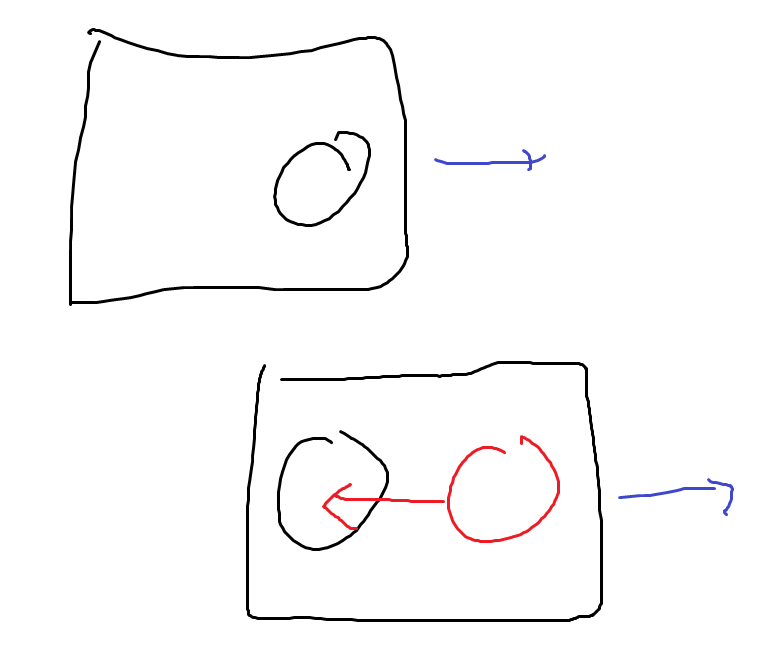
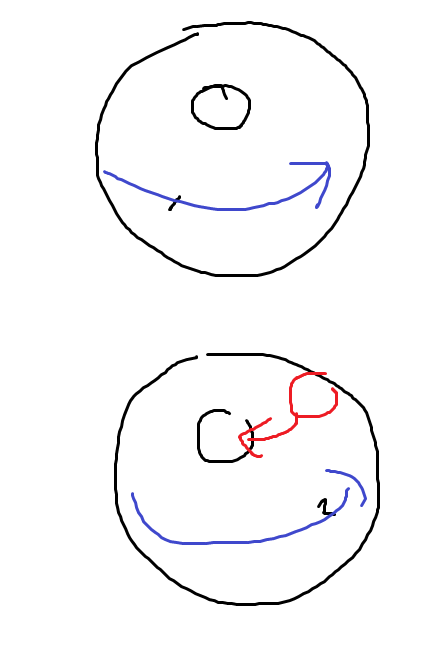
[!question]- 가상적인 힘이 생기는 이유가 무엇인가?{title}

물체는 가만히 있는데, 계가 움직여버린다. 따라서 이 계 안에 서있는 관측자는 공이 갑자기 뒤로 가는 것 처럼 보인다.

물체는 가만히 있는데, 계가 움직여버린다. 따라서 이 계안에 서있는 관측자는, 공이 갑자기 원호를 그리는 것 처럼 보인다.