고전역학 4. Projectile motion

Analytical mechanics/Fowles, Grant R. (7판)의 내용입니다.

Projectile motion

공기 저항을 받지 않는 포사체 운동을 예측하는 방법에 대해서 알아보자. 초기 속도가 \(\mathbf{v_{0}}\)으로 주어지고, \(t=0\)일 때 \((0, 0, 0)\)에서 포사체 운동을 시작한다. 이 입자가 받는 힘은 중력밖에 없으므로 미분 방정식은 \(m \ddot{ \mathbf{r}}=-mg \mathbf{k}\)와 같다. 양 변을 m으로 나누고, 각 변을 t에 대해 적분하여 미분방정식을 풀 수 있다.

\[\ddot{ \mathbf{r}}=-g \mathbf{k} \implies\dot{ \mathbf{r} } = -gt \mathbf{k} + \mathbf{v}_{0} =>\displaystyle \mathbf{r} = -\frac{1}{2} gt^2 \mathbf{k}+ \mathbf{v_{0}}t+\mathbf{r_{0}}\]

t=0일 때 \((0, 0, 0)\)으로 잡으면 \(\mathbf{r_{0}}\)을 지울 수 있고, 초기 속도 벡터가 지면과 이루는 각도를 \(\alpha\)라고 해서 \(\mathbf{v_{0}}=(v_{0}\cos \alpha, 0, v_{0}\sin \alpha)\)로 풀면 다음과 같다.

\[\mathbf{r}=\mathbf{i}v_{0}\cos \alpha + \mathbf{k}\left( v_{0}\sin \alpha- \frac{1}{2 }gt^2 \right)=\left( v_{0}\cos \alpha, 0, v_{0}\sin \alpha- \frac{1}{2} gt^2 \right)\]

포사체 운동에서 우리가 가장 알고싶은 값은, \(z_{max}\), \(x_{max}\), \(x-z\)의 관계(공간상에서 경로) 이다.

• \(x-z\)의 관계 (공간 상의 경로)
  • \(x=v_{0}\cos \alpha t\)이므로 \(\displaystyle t=\frac{x}{v_{0}\cos \alpha}\)를 \(z(t)\)에 넣으면 다음과 같다.
  • \(\displaystyle z=\tan \alpha x- \frac{g}{2v_{0}^2\cos^2\alpha}x^2\)
  • 따라서 공간에서의 경로는 포물선을 그린다.
• \(z_{max}\)
  • z성분의 속도가 0일 때 시간을 구해서, \(z(t)\)에 대입한다.
  • \(\displaystyle \dot{\mathbf{r}}=\mathbf{i} v_{0}\cos \alpha+ \mathbf{k}(v_{0}\sin \alpha-gt) \implies v_{0}\sin \alpha-gt_{high}=0 \implies t_{high}=\frac{{v_{0}\sin \alpha}}{g}\)
  • \(\displaystyle z_{max}=z(t_{high})=v_{0}\sin \alpha\left( \frac{{v_{0}\sin \alpha}}{g} \right)-\frac{1}{2}g\left( \frac{{v_{0}\sin \alpha}}{g} \right)^2= \frac{{v_{0}^2\sin^2\alpha}}{2g}\)
• \(x_{max}\)
  • 경로가 포물선이므로, 지면에서 출발해서 지면으로 도달한 시간은 정확히 \(t_{high}\)의 두배다.
  • \(\displaystyle x_{max}=x(2t_{high})=v_{0}\cos \alpha \cdot \frac{2v_{0}\sin \alpha}{g}= \frac{v_{0}^2\sin 2\alpha}{g}\)
  • 따라서 \(\alpha\)가 45도일 때, \(x_{max}\)는 최대값을 갖는다.

Damped projectile motion

선형 공기저항을 받는 포사체 운동에 대해 알아보자. \(t=0\)일 때 \(\mathbf{r_{0}}=(0,0,0)\)에서 시작하여 초기 속도 \(\mathbf{v_{0}}=\dot{\mathbf{r_{0}}}=(\dot{x_{0}},\dot{y_{0}},\dot{z_{0}})=(v_{0}\cos \alpha,0,v_{0}\sin \alpha)\)를 갖도록 설정한다. 입자는 중력, 공기저항만 받으므로 미분 방정식은 \(m \ddot{\mathbf{r}}=-c_{1}\mathbf{v}-mg\mathbf{k}\)와 같다. 식의 간소화를 위해, \(c_{1}=m\gamma\)로 잡고 m을 소거하면 다음과 같다. \(\ddot{\mathbf{r}}=-\gamma\dot{\mathbf{r}}-g\mathbf{k} \implies (\ddot{x},\ddot{y},\ddot{z})=-\gamma(\dot{x},\dot{y},\dot{z})-g(0,0,1)\), 각 성분별로 나누면 3개의 상미분 방정식을 얻을 수 있다.

\[\ddot{x}=-\gamma\dot{x}\] \[\ddot{y}=-\gamma\dot{y}\] \[\ddot{z}=-\gamma\dot{z}-g\]

\(\dot{x}\), \(\dot{y}\)는 바로 \(\dot{x}=\dot{x_{0}}e^{-\gamma t}\), \(\dot{y}=\dot{y_{0}}e^{-\gamma t}\) 꼴임을 알 수 있다. \(\dot{z}\)는 \(\displaystyle \ddot{z}=-\gamma \left( \dot{z}-\frac{g}{\gamma} \right)\) 꼴로 쓰고 \(\displaystyle \dot{z}-\frac{g}{\gamma}=p\)로 치환하면 구할 수 있다.

\[\dot{p}=-\gamma p \implies p= p_{0}e^{-\gamma t}\]

이때 \(\displaystyle p_{0}=\dot{z_{0}}-\frac{g}{\gamma}\)이므로 \(\displaystyle \dot{z}-\frac{g}{\gamma}=(\dot{z_{0}}-\frac{g}{\gamma})e^{-\gamma t}\) 이다. \(\displaystyle \dot{x}=\dot{x_{0}}e^{-\gamma t} \implies \frac{dx}{dt} = \dot{x_{0}}e^{-\gamma t}\) 이므로, \(dt\)를 우변으로 넘기고 \(0\)부터 \(t\)까지 적분하면 다음과 같다.

\[\int ^{x}_{x_{0}} \, dx = \int ^t_{0} \dot{x_{0}}e^{-\gamma t} \, dt \implies x-x_{0}= \frac{\dot{x_{0}}}{\gamma}(1-e^{-\gamma t})\]

\(x_{0}=0\), \(\dot{y}=0\)으로 잡았으므로, \(x_{0}\)과 \(y\)항은 무시할 수 있다. \(z\)도 똑같이 미분하면 최종적으로 다음 결과를 얻는다.

• \(\displaystyle z(t)=\left( \frac{\dot{z_{0}}}{\gamma} + \frac{g}{\gamma^2} \right)(1-e^{-\gamma t})-\frac{g}{\gamma}t\)
• \(\displaystyle x(t)= \frac{\dot{x_{0}}}{\gamma}(1-e^{-\gamma t})\)
• \(\displaystyle \mathbf{r}(t)=(x(t), 0, z(t))\)

사정거리 \(x_{max}\)

사정거리 \(x_{max}\)은 \(z(t_{max})=0\)일 때 식과 \(x(t_{max})=x_{max}\)일 때 식을 잘 연립해서 \(x_{max}\)에 대해 방정식을 풀면 구할 수 있다. 그 미분 방정식은 \(\displaystyle \left( \dot{\frac{z_{0}}{\gamma}} + \frac{g}{\gamma^2}\right){\frac{\gamma x_{max}}{\dot{x_{0}}}}+\frac{g}{\gamma^2}\ln(1- {\frac{\gamma x_{max}}{\dot{x_{0}}}})=0\) 이다. \(\ln(1-u)=-u - \frac{u^2}{2} - \frac{u^3}{3} - \dots\) 테일러 급수를 사용해서 급수전개하면 해를 구할 수 있다. 계산 팁은, 한번에 구하려 하지 말고 2차 근사를 하고, 그 결과를 3차 근사에 이용하고, 그 결과를 4차 근사에 이용하고, 이런 재귀적인 방법으로 해에 점점 다가가야 한다.

1. 2차 근사
   • \(\displaystyle \left( \dot{\frac{z_{0}}{\gamma}} + \frac{g}{\gamma^2}\right){\frac{\gamma x_{max}}{\dot{x_{0}}}}+\frac{g}{\gamma^2}\left( - \frac{{\gamma x_{max}}}{\dot{x_{0}}} - \frac{1}{2} \left(\frac{{\gamma x_{max}}}{\dot{x_{0}}}\right)^2 + O(\gamma^3)\right)=0\)
   • 이때, \(O(\gamma^3)\)은 \(\gamma^3\)항을 의미한다.
   • \(\displaystyle \frac{{2 \dot{z_{0}} \dot{x_{0}}}}{g} - x_{max} + O(\gamma) = 0 \implies x_{max} = \frac{{2 \dot{z_{0}} \dot{x_{0}}}}{g} + O(\gamma)\)
2. 3차 근사
   • \(\displaystyle \left( \dot{\frac{z_{0}}{\gamma}} + \frac{g}{\gamma^2}\right){\frac{\gamma x_{max}}{\dot{x_{0}}}}+\frac{g}{\gamma^2}\left( - \frac{{\gamma x_{max}}}{\dot{x_{0}}} - \frac{1}{2} \left(\frac{{\gamma x_{max}}}{\dot{x_{0}}}\right)^2 - \frac{1}{3} \left(\frac{{\gamma x_{max}}}{\dot{x_{0}}}\right)^3+ O(\gamma^4)\right)=0\)
   • \(\displaystyle \dot{\frac{z_{0}}{ g }} - \frac{x_{max} }{ 2\dot{x_{0}} }- \frac{x_{max}^2 }{ 3\dot{x_{0}}^2 } \gamma + O(\gamma^2)=0\)
   • 여기서, 2차 근사에서 얻었던 \(\displaystyle x_{max} = \frac{{2 \dot{z_{0}} \dot{x_{0}}}}{g} + O(\gamma)\) 값을 대입한다.
   • \(\displaystyle \dot{\frac{z_{0}}{ g }} - \frac{ 1}{ 2\dot{x_{0}} } \left( \frac{{2 \dot{z_{0}} \dot{x_{0}}}}{g} + O(\gamma) \right) - \frac{1 }{ 3\dot{x_{0}}^2 } \left(\frac{{2 \dot{z_{0}} \dot{x_{0}}}}{g} + O(\gamma)\right)^2 \gamma + O(\gamma^2)=0\)
   • \(\displaystyle O(\gamma)=- \frac{{8 \dot{x_{0}} \dot{z_{0}}^2}}{3g^2} + O(\gamma^2)\)
   • 구한 값을 활용하여, 해를 더 정교하게 근사한다.
   • \(\therefore ~ \displaystyle x_{max} = \frac{{2 \dot{z_{0}} \dot{x_{0}}}}{g} - \frac{{8 \dot{x_{0}} \dot{z_{0}}^2}}{3g^2}r + O(\gamma^2)\)
3. 4차 근사, 5차 근사, …. 를 반복하면 더 정교한 해를 얻는다.

지구 회전 효과까지 고려하는 경우

우리는 지구 안에서 살고, 지구 안에서 운동분석을 하기 때문에 지구의 영향에서 벗어날 수 없다. 지구의 각속도는 약 \(7.27 \times 10^{-5} rad / s\) 으로 매우 작다. 따라서 평범한 스케일에서는 그냥 관성 좌표계라고 생각하고 분석해도 된다. 하지만 지구 스케일의 무언가(미사일 발사)를 해야할 때는 지구 회전의 효과를 반드시 고려해주어야 한다.

용어

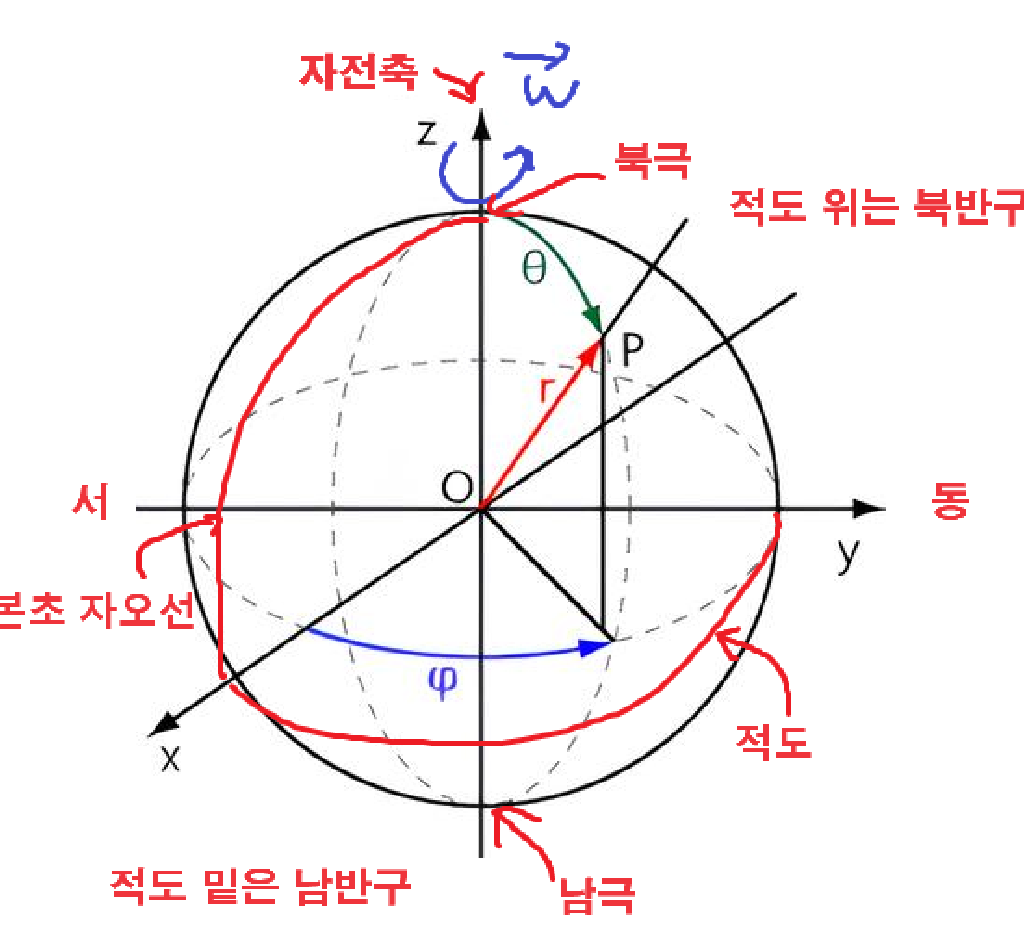
지구의 좌표를 효과적으로 분석하기 위해, 지구의 중심을 원점으로, 지구 각속도의 방향을 z축으로, x축을 영국의 그리니티 천문대를 지나도록 하는 구면 좌표계를 설정해보자.

• \(\theta\), \(\phi\) : 각각 위도, 경도
  • 각 \(\theta\)와 \(\phi\)는 0~180도만 올 수 있으며, \(+\theta\) = 북위, \(-\theta\) = 남위, \(+\phi\) = 동경, \(-\phi\) = 서경 이라고 부름.
  • 즉 지구상의 \((r_{e}, -37, 128)\) 좌표는 남위 37도, 동경 128도라고 부른다.
• 적도 : x, y 평면과 지구가 만나는 선.
• 본초 자오선 : x, z 평면과 지구가 만나는 선.
• 남반구 : 적도를 기준으로 남쪽의 반구
• 북반구 : 적도를 기준으로 북쪽의 반구
• 연추 : 공중에 고정되어 매달려있는 추.

미사일을 발사할 때 낙하 지점 예측

결국 지구 스케일에서 우리가 가장 원하는 작업은 미사일을 발사했을 때 어디 지점에 떨어질 지 예측하는 것과 같다. 즉, 어느 좌표에서 어떤 질량의 물체를 어떤 초기 속도로 발사하면, 어느 지점에 떨어질까? 를 예측하는 문제가 된다.

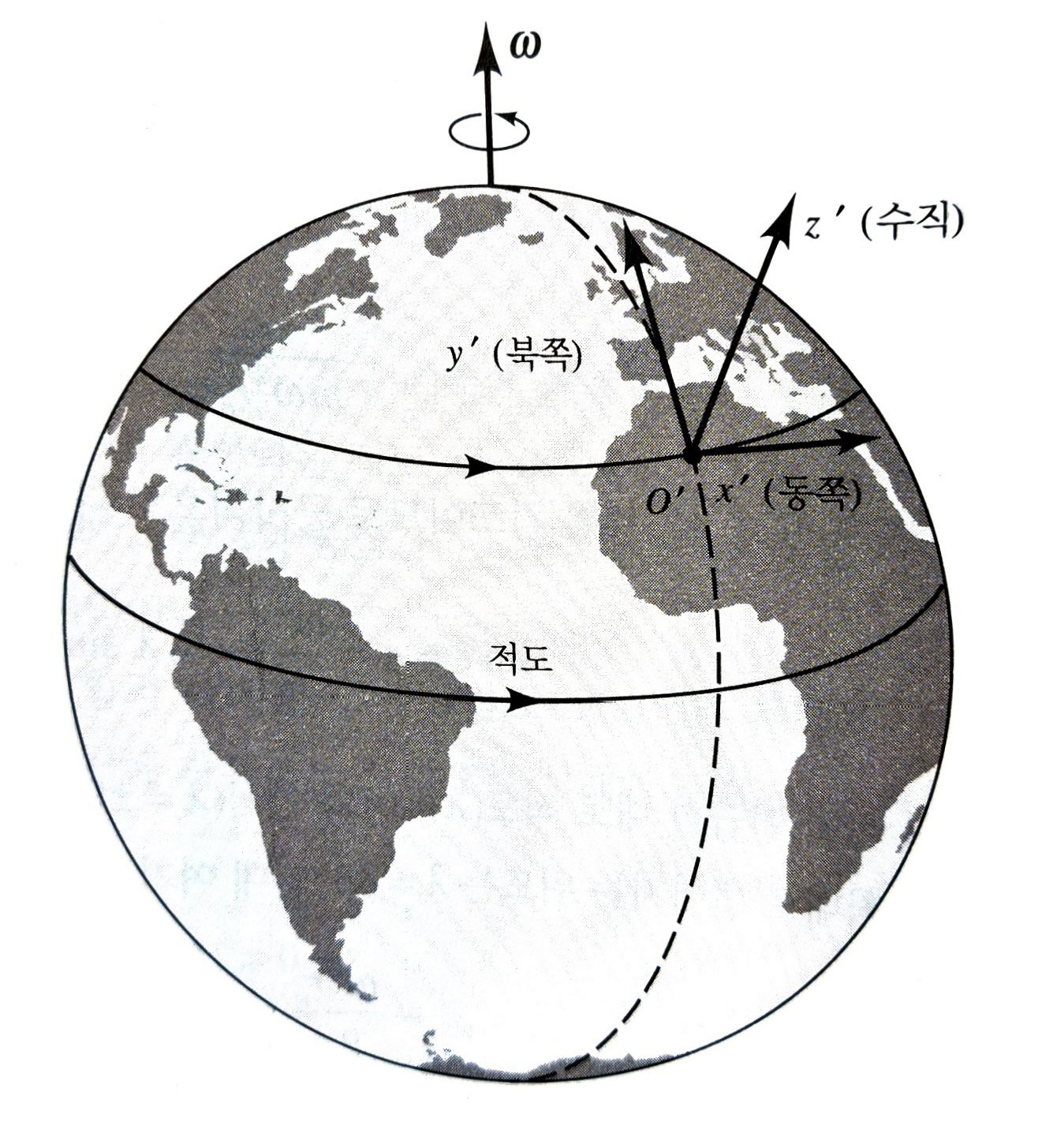
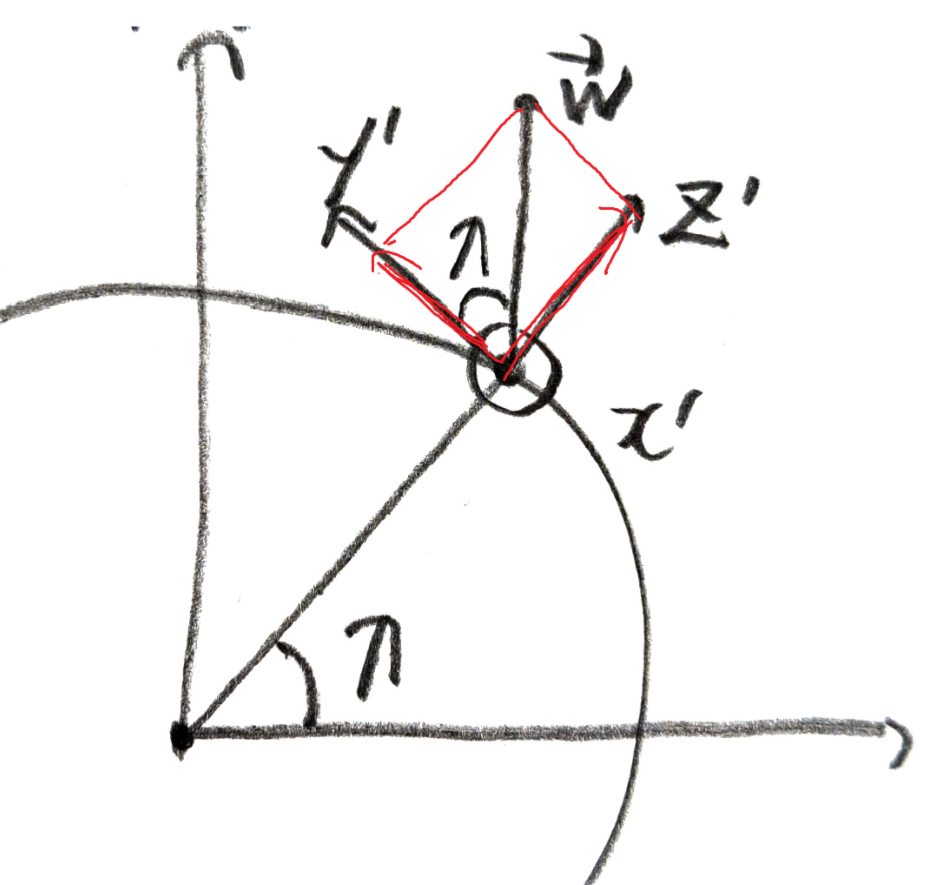
\((r, \theta, \phi)\) 좌표에서 병진 + 회전하는 비관성 좌표계의 원점을 설정하고, 그 좌표계 원점에서 미사일을 발사하여 어느 좌표에 떨어질 지 계산해내면 된다. 회전좌표계를 잡을 때, 위 그림과 같이 z축은 곡면과 수직하게, x축은 적도와 평행하고 +방향, y축은 본초 자오선과 평행하고, +방향으로 잡는게 직관적이다.

\[\mathbf{a}=\mathbf{a}'+\mathbf{\dot{\omega}} \times \mathbf{r}' + 2 \mathbf{\omega} \times \mathbf{v}' + \mathbf{\omega} \times (\mathbf{\omega} \times \mathbf{r}') + \mathbf{A_{0}}\]

가속도는 위와 같이 구할 수 있고, 지구의 회전속도가 일정하므로 가로 가속도를 제거하면 \(\mathbf{a}=\mathbf{a}'+2 \mathbf{\omega} \times \mathbf{v}' + \mathbf{\omega} \times (\mathbf{\omega} \times \mathbf{r}') + \mathbf{A_{0}}\)와 같다. \(\mathbf{F} = m\mathbf{a}\)에 대입하면, 다음 방정식을 얻는다.

\[\mathbf{F}-m \mathbf{A_{0}} - 2 m\mathbf{\omega} \times \mathbf{v}' -m \mathbf{\omega} \times (\mathbf{\omega} \times \mathbf{r}') = m \mathbf{a}'\]

여기서 \(\mathbf{F}\)는 물체가 받는 실제 힘이다. 중력 \(m \mathbf{g}\), 공기저항 등의 효과를 생각할 수 있다. 간단하게 구하기 위해, 공기저항을 무시하면 \(\mathbf{F}=m\mathbf{g_{0}}\), 각속도는 작은 값인데, 그 값이 두번 곱해진 구심 가속도 항은 아주 작다. 이것 까지 무시하면 \(m \mathbf{a}' = m \mathbf{g_{0}}-m \mathbf{A_{0}}-2m \mathbf{\omega} \times \mathbf{v}'\)와 같다. m을 약분하고, \(g_0\)과 \(A_{0}\) 벡터합의 결과는 실제로 받고있는 중력가속도 벡터 \(\mathbf{g}\)이므로 다음과 같다.

\[\mathbf{a}' = \mathbf{g} - 2m \omega \times \mathbf{v}'\]

\[\mathbf{a}'= \ddot{r}'\] \[\mathbf{v}'=\dot{r}'\] \[\mathbf{r}'=(x',y',z')\] \[\mathbf{g}= -g\hat{k}'\] \[\mathbf{\omega}=\hat{j}' \omega \cos \lambda + \hat{k}' \omega \sin \lambda\]

\(\lambda\)=위도라 하면, 세개의 미분방정식을 뽑아낼 수 있다.

[!note]- 미분 방정식 계산 과정{title}

\[\ddot{x}'=-2w(\cos \lambda \dot{z}' - \sin \lambda \dot{y}')\] \[\ddot{y}'=-2\omega \sin \lambda \dot{x}'\] \[\ddot{z}'=-g+2\omega \cos \lambda \dot{x}'\]

\(\ddot{y}'\)와 \(\ddot{z}'\)의 양 변을 각각 t에 대해 미분해서, \(\ddot{x}'\) 방정식에 대입한다.

\[\dot{y}'- \dot{y_{0}}'=-2\omega \sin \lambda x'\] \[\dot{z}' - \dot{z_{0}}' = -gt + 2\omega \cos \lambda x'\]

\(x_{0}'=0\)이라고 가정함.

\[\ddot{x}'=-2w(\cos \lambda (-gt + 2\omega \cos \lambda x' + \dot{z_{0}}') - \sin \lambda (-2\omega \sin \lambda x' + \dot{y_{0}}'))\]

이때, \(\omega^2 \simeq 0\)이므로, 소거하고 정리한다.

\[\ddot{x}'=2\omega gt\cos \lambda - 2\omega(\dot{z_{0}}'\cos \lambda - \dot{y_{0}}' \sin \lambda)\] \[\dot{x}'=\omega gt^2\cos \lambda-2\omega t(\dot{z_{0}}'\cos \lambda - \dot{y_{0}}' \sin \lambda)+ \dot{x_{0}}'\] \[x'(t)= \frac{1}{3} \omega gt^3\cos \lambda-\omega t^2(\dot{z_{0}}'\cos \lambda - \dot{y_{0}}' \sin \lambda)+ \dot{x_{0}}'t\]

이제 이 값을, \(\dot{y}'- \dot{y_{0}}'=-2\omega \sin \lambda x'\)와 \(\dot{z}' - \dot{z_{0}}' = -gt + 2\omega \cos \lambda x'\)에 넣어주고 \(\omega^2\)항을 소거하고 t에 대해 적분하면 \(y'\)와 \(z'\)도 t에 대한 함수 꼴로 구할 수 있다.

\[y'(t)= \dot{y_{0}}'t - \omega \sin \lambda \dot{x_{0}}' t^2 + y_{0}'\] \[z'(t) = \dot{z_{0}}'t - \frac{1}{2} gt^2 + \omega \cos \lambda \dot{x_{0}}' t^2 + z_{0}'\]