고전역학 1. 좌표계

Analytical mechanics/Fowles, Grant R. (7판)의 내용입니다.

Rectangular coordinate (직교좌표계)

기저 벡터가 서로 직교하는 좌표계.

[!example]- 2차원 직교 좌표계{title}

\[\mathbb{R}^2 = \{ (x, y) | x, y \in \mathbb{R} \}\]

[!example]- 3차원 직교 좌표계{title}

\[\mathbb{R}^3 = \{ (x, y, z) | x, y, z \in \mathbb{R} \}\]

Polar coordinate (극좌표계)

\(\displaystyle \hat{e}_{r}, \hat{e}_{\theta}, \frac{d\hat{e}_r}{dt}, \frac{d\hat{e}_\theta}{dt}\) 알면 \(\vec{r} = r \hat{e}_{r}\)을 통해 \(\vec{v}, \vec{a}\) 유도 가능.

Cylindrical coordinate (원통 좌표계)

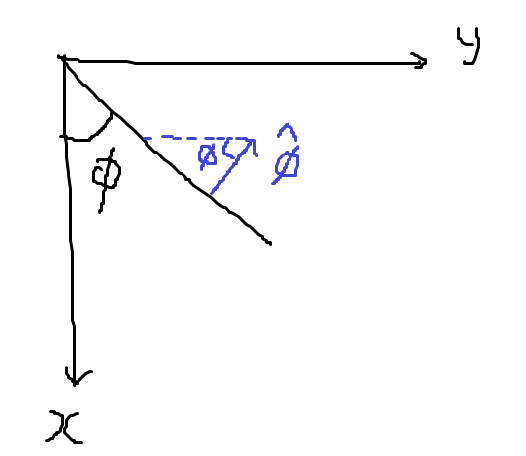
\((x, y, z)\) 대신 \((s, \phi, z)\) 좌표를 사용한다.

[!question]- How to Transform{title}

\[\hat{s} = \cos \phi \hat{x} + \sin \phi \hat{y}\] \[\hat{\phi} = -\sin \phi \hat{x} + \cos \phi \hat{y}\] \[\hat{z} = \hat{z}\]

기저벡터를 구해 Linear Transform Matrix를 구하고, (Matrix의 Column = Bais) Inverse Matrix를 취해 좌표계 변환 행렬을 얻는다.

이 행렬과, \((x, y, z)\) 좌표에서 표현된 벡터를 행렬-벡터곱 하면 \((s, \phi, z)\) 좌표계로 변환된 좌표를 얻을 수 있다.

\[\text{선형 변환} = \begin{bmatrix} \cos \phi & -\sin \phi & 0 \\ sin \phi& \cos \phi & 0\\ 0& 0&1 \end{bmatrix}\] \[\text{좌표계 변환} = \begin{bmatrix} \cos \phi & \sin \phi & 0 \\ -sin \phi& \cos \phi & 0\\ 0& 0&1 \end{bmatrix}\]

[!tip] Tip{title} 역행렬을 구하려면, 행렬을 전치\(^T\)하면 된다. 행렬이 세 Column이 직교하는 직교 행렬이므로, 역행렬 = 전치행렬이 성립한다.

[!note]- \(\displaystyle \frac{{d \hat{s}}}{dt}, ~\frac{{d \hat{\phi}}}{dt}, ~\frac{{d \hat{z}}}{dt}\){title}

\[\frac{{d \hat{s}}}{dt} = \dot{\phi} \hat{\phi}, ~~\frac{{d \hat{\phi}}}{dt} = -s \dot{s} \hat{s}, ~~\frac{{d \hat{z}}}{dt} = 0\]

[!question] Why?{title}

\[\frac{{d \hat{s}}}{dt} = \frac{d}{dt} (\cos \phi \hat{x} + \sin \phi \hat{y})\] \[= -\sin \phi \cdot \frac{{d \phi}}{dt} \hat{x} + \cos \phi \cdot \frac{{d \phi}}{dt} \hat{y}= \frac{{d \phi}}{dt} \hat{\phi} = \dot{\phi} \hat{\phi}\] \[\frac{{d \hat{\phi}}}{dt} = \frac{d}{dt}(-\sin \phi \hat{x} + \cos \phi \hat{y})\] \[= -\cos \phi \cdot \frac{{d\phi}}{dt} \hat{x} - \sin \phi \cdot \frac{{d \phi}}{dt} \hat{y} = - \frac{ds}{dt} \hat{s} = -s \dot{s} \hat{s}\]

[!note]- \(\vec{r}\), \(\vec{v}\), \(\vec{a}\){title}

\[\vec{r} = s \hat{s} + z \hat{z}\] \[\vec{v} = \dot{s} \hat{s} + s \dot{\phi} \hat{\phi} + \dot{z} \hat{z}\] \[\vec{a} = (\ddot{s} - s \dot{\phi}^2) \hat{s} + (r \ddot{\phi} + 2 \dot{r} \dot{\theta}) \hat{\theta} + \ddot{z} \hat{z}\]

[!question] Why?{title}

\[\vec{v} = \frac{{d \vec{r}}}{dt} = \frac{d}{dt}(s \hat{s} + z \hat{z})\] \[= \frac{ds}{dt} \hat{s} + s \frac{{d \hat{s}}}{dt} + \frac{dz}{dt} \hat{z}\] \[= \dot{s} \hat{s} + s \dot{\phi} \hat{\phi} + \dot{z} \hat{z}\] \[\vec{a} = \frac{{d \vec{v}}}{dt} = \frac{d}{dt} (\dot{s} \hat{s} + s \dot{\phi} \hat{\phi} + \dot{z} \hat{z})\] \[= \ddot{s} \hat{s} + s\frac{{d \hat{s}}}{dt} + \dot{s} \dot{\phi} \hat{\phi} + s \ddot{\phi} \hat{\phi} + s \dot{\phi} \frac{{d \hat{\phi}}}{dt} + \ddot{z} \hat{z}\] \[= \ddot{s} \hat{s} + \dot{s} \dot{\phi} \hat{\phi} + \dot{s} \dot{\phi} \hat{\phi} + s \ddot{\phi} \hat{\phi} - s \dot{\phi}^2 \hat{\phi} + \ddot{z} \hat{z}\] \[= (\ddot{s} - s \dot{\phi}^2) \hat{s} + (r \ddot{\phi} + 2 \dot{r} \dot{\theta}) \hat{\theta} + \ddot{z} \hat{z}\]

[!note]- \(d \vec{r}\), \(dV\){title}

\[d \vec{r} = (ds, sd\phi, dz)= ds \hat{s} + s d\phi \hat{\phi} + dz \hat{z}\] \[dV = (ds) (s d\phi) (dz)\]

미소 변화량은 길이가 조금 변한 것. 원래 길이 성분의 미소 변화량은 그냥 길이가 조금 변한거니까 \(ds\), \(dz\) 그대로 사용한다.

하지만 각도 변화량은 길이 변화량, 즉 호의 변화량으로 생각해서 \(s d\phi\)를 사용해야 한다.

그림을 그려보고, 조금 변한다는 것의 의미를 생각하면 금방 알 수 있다.

[!note]- Differential Operator{title}

\[\nabla = \left( \frac{\partial}{\partial s}, \frac{1}{s} \frac{\partial}{\partial \phi}, \frac{\partial}{\partial z} \right)\]

[!question] \(\frac{1}{s}\) 붙는건 뭐냐?{title} \(d f(s, \phi, z)\)를 정의하는 과정을 생각해보면 된다.

\[d f(s, \phi, z) = f(s+ds, \phi, z) - f(s, \phi, z) + \dots\] \[= \left( \frac{{\partial f}}{\partial s} \right)ds + \frac{1}{s} \left( \frac{{\partial f}}{\partial \phi} \right) s d\phi + \left( \frac{{\partial f}}{\partial z} \right)dz\] \[= \left( \frac{\partial}{\partial s}, \frac{1}{s} \frac{\partial}{\partial \phi}, \frac{\partial}{\partial z} \right) f \cdot d \vec{r}\] \[= \nabla f \cdot d \vec{r}\]

\[\nabla \Phi = \frac{{\partial \Phi}}{\partial s} \hat{s} + \frac{1}s \frac{{\partial \Phi}}{\partial \phi} \hat{\phi} + \frac{{\partial \Phi}}{\partial z} \hat{z}\] \[\nabla \cdot \vec{A} = \frac{1}{s} \left( \frac{\partial}{\partial s} (s A_{s}) + \frac{\partial A_{\phi}}{\partial \phi} + \frac{\partial}{\partial z} (sA_{z}) \right)\] \[\nabla \times \vec{A} = \frac{1}{s} \begin{vmatrix} \hat{s} & s \hat{\phi} & \hat{z}\\ \frac{\partial}{\partial s}& \frac{\partial}{\partial \phi} & \frac{\partial}{\partial z}\\ A_{s} & s A_{\phi} & A_{z}\end{vmatrix}\] \[\nabla^2 \Phi = \frac{1}{s} \left[ \frac{\partial}{\partial s} \left( s \frac{{\partial \Phi}}{\partial s} \right) + \frac{\partial}{\partial \phi} \left( \frac{1}{s} \frac{{\partial \Phi}}{\partial \phi} \right) + \frac{\partial}{\partial z} \left( s \frac{{\partial \phi}}{\partial z} \right) \right]\]

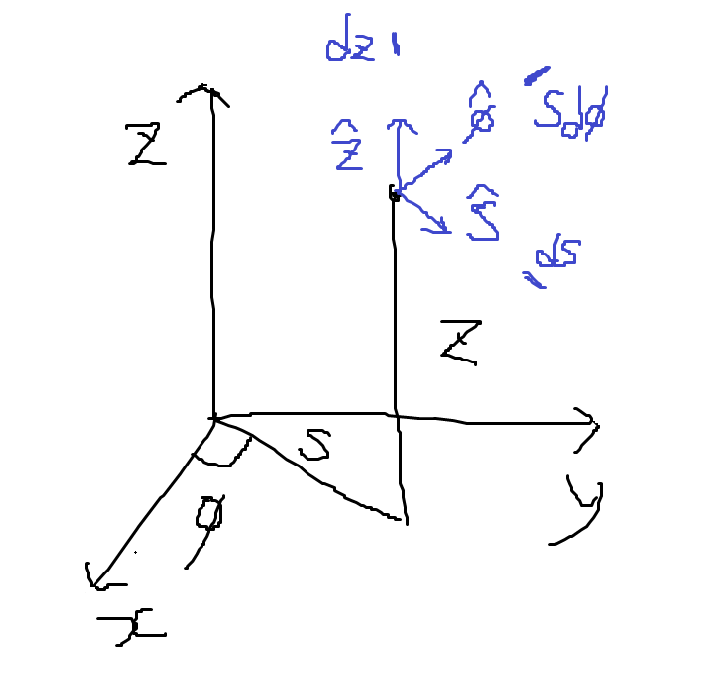
Spherical coordinate (구면 좌표계)

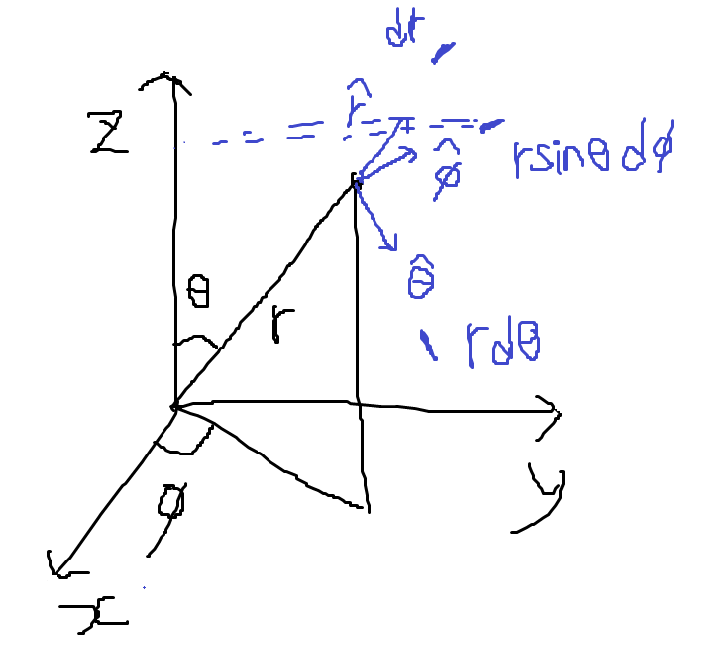
\((x, y, z)\) 대신 \((r, \theta, \phi)\) 좌표를 사용한다.

[!question]- How to Transform{title}

\[\hat{r} = \sin \theta \cos \phi \hat{x} + \sin \theta \sin \phi \hat{y} + \cos \theta \hat{z}\] \[\hat{\theta} = \cos \theta \cos \phi \hat{x} + \cos \theta \sin \phi \hat{y} - \sin \theta \hat{z}\] \[\hat{\phi} = -\sin \phi \hat{x} + \cos \phi \hat{y}\]

그림을 그려서 x, y, z축에 단위벡터를 사영해보면서 어떤 x 성분이 \(\hat{r}\)를 만들고를 따져보면 알 수 있다.

특히 \(\hat{\phi}\)은 \(xy\) 평면을 그려보면 더 쉽게 알 수 있다.

기저벡터를 구해 Linear Transform Matrix를 구하고, (Matrix의 Column = Bais) Inverse Matrix를 취해 좌표계 변환 행렬을 얻는다.

이 행렬과, \((x, y, z)\) 좌표에서 표현된 벡터를 행렬-벡터곱 하면 \((s, \phi, z)\) 좌표계로 변환된 좌표를 얻을 수 있다.

\[\text{선형 변환} = \begin{bmatrix} \sin \theta \cos \phi & \cos \theta \cos \phi & -\sin \phi\\ \sin \theta \sin \phi& \cos \theta \sin \phi & \cos \phi\\ \cos \theta& -\sin \theta&0 \end{bmatrix}\] \[\text{좌표계 변환} = \begin{bmatrix} \sin \theta \cos \phi & \sin \theta \sin \phi & \cos \theta\\ \cos \theta \cos \phi& \cos \theta \sin \phi & -\sin \theta\\ -\sin \phi& \cos \phi&0 \end{bmatrix}\]

[!tip] Tip{title} 역행렬을 구하려면, 행렬을 전치\(^T\)하면 된다. 행렬이 세 Column이 직교하는 직교 행렬이므로, 역행렬 = 전치행렬이 성립한다.

[!note]- \(\displaystyle\frac{{d \hat{r}}}{dt}, ~\frac{{d \hat{\theta}}}{dt}, ~\frac{{d \hat{\phi}}}{dt}\){title}

\[\frac{{d \hat{r}}}{dt} = \dot{\theta} \hat{\theta}+ \sin \theta \dot{\phi} \hat{\phi}\] \[\frac{{d \hat{\theta}}}{dt} = - \dot{\theta} \hat{r} + \cos \theta \dot{\phi} \hat{\phi}\] \[\frac{{d \hat{\phi}}}{dt} = - \dot{\phi}\sin \theta \hat{r} + - \dot{\phi}\cos \theta \hat{\theta}\]

[!question] Why?{title}

\[\frac{{d \hat{r}}}{dt} = \frac{d}{dt} (\sin \theta \cos \phi \hat{x} + \sin \theta \sinh \phi \hat{y} + \cos \theta \hat{z})\] \[= \cos \theta \cos \phi \cdot \dot{\theta} \hat{x} - \sin \theta \sin \phi \cdot \dot{\phi} \hat{x} + \cos \theta \sin \phi \cdot \dot{\theta} \hat{y} + \sin \theta \cos \phi \cdot \dot{\phi} \hat{y} - \sin \theta \cdot \dot{\theta} \hat{z}\] \[= \dot{\theta} (cos \theta \cos \phi \hat{x} + \cos \theta \sin \phi \hat{y} - \sin \theta \hat{z}) + \sin \theta \dot{\phi}( - \sin \phi \hat{x} + \cos \phi \hat{y})\] \[= \dot{\theta} \hat{\theta} + \sin \theta \dot{\phi} \hat{\phi}\] \[\frac{{d \hat{\theta}}}{dt} = \frac{d}{dt}(\cos \theta \cos \phi \hat{x} + \cos \theta \sin \phi \hat{y} - \sin \theta \hat{z})\] \[= -\sin \theta \cos \phi \cdot \dot{\theta} \hat{x} - \cos \theta \sin \phi \cdot \dot{\phi} \hat{x} - \sin \theta \sin \phi \cdot \dot{\theta} \hat{y} + \cos \theta \cos \phi \cdot \dot{\phi} \hat{y} - \cos \theta \cdot \dot{\theta} \hat{z}\] \[= - \dot{\theta} (\sin \theta \cos \phi \hat{x} + \sin \theta \sin \phi \hat{y} + \cos \theta \hat{z}) + \cos \theta \dot{\phi}(-\sin \phi \hat{x} + \cos \phi \hat{y})\] \[= - \dot{\theta} \hat{r} + \cos \theta \dot{\phi} \hat{\phi}\] \[\frac{{d \hat{\phi}}}{dt} = \frac{d}{dt}(-\sin \phi \hat{x} + \cos \phi \hat{y})\]

\(\sin \theta \hat{r}\)과 \(\cos \theta \hat{\theta}\)를 구해보자.

\[\sin \theta \hat{r} = \sin^2\theta \cos \phi \hat{x} + \sin^2\theta \sin \phi \hat{y} + \sin \theta \cos \theta \hat{z}\] \[\cos \theta \hat{\theta} = \cos^2\theta \cos \phi \hat{x} + \cos^2\theta \sin \phi \hat{y} - \sin \theta \cos \theta \hat{z}\]

두개를 더하면 다음과 같다.

\[\sin \theta \hat{r} + \cos \theta \hat{\theta} = \cos \phi \hat{x} + \sin \phi \hat{y}\]

따라서, \(\frac{{d \hat{\phi}}}{dt}\)는 다음과 같다.

\[\frac{{d \hat{\phi}}}{dt} = - \dot{\phi} \sin \theta \hat{r} - \dot{\phi} \cos \theta \hat{\theta}\]

[!note]- \(\vec{r}\), \(\vec{v}\), \(\vec{a}\){title}

\[\vec{r} = r \hat{r}\] \[\vec{v} = \dot{r} \hat{r} + r \dot{\theta} \hat{\theta} + r \dot{\phi} \sin \theta \hat{\phi}\] \[\vec{a} = \frac{{d \vec{v}}}{dt} = \dots\]

[!question] Why?{title}

\[\vec{v} = \frac{{d \vec{r}}}{dt} = \frac{d}{dt} (r \hat{r})\] \[= \dot{r} \hat{r} + r \frac{{d \vec{r}}}{dt}\] \[= \dot{r} \hat{r} + r \dot{\theta} \hat{\theta} + r \dot{\phi} \sin \theta \hat{\phi}\] \[\vec{a} = \frac{{d \vec{v}}}{dt} = \frac{d}{dt} (\dot{r} \hat{r} + r \dot{\theta} \hat{\theta} + r \dot{\phi} \sin \theta \hat{\phi})\] \[= \ddot{r} \hat{r} + \dot{r} \frac{{d \hat{r}}}{dt} + \dot{r} \dot{\theta} \hat{\theta} + r \ddot{\theta} \hat{\theta} + r \dot{\theta} \frac{{d \hat{\theta}}}{dt} + \dot{r} \dot{\phi} \sin \theta \hat{\phi} + r \ddot{\phi} \sin \theta \hat{\phi} + r \dot{\phi} \cos \theta \cdot \dot{\theta} \hat{\phi} + r \dot{\phi} \sin \frac{\theta {d \hat{\phi}}}{dt}\] \[= \dots\]

[!note]- \(d \vec{r}\), \(dV\){title}

\[d \vec{r} = (dr, r d\theta, r \sin \theta d\phi)= dr \hat{r} + r d\theta \hat{\theta} + r\sin \theta d\phi \hat{\phi}\] \[dV = (dr) (r d \theta) (r\sin \theta d\phi) = r^2\sin \theta dr d\theta d\phi\]

미소 변화량은 길이가 조금 변한 것.

원래 길이 성분의 미소 변화량은 그냥 길이가 조금 변한거니까 \(ds\), \(dz\) 그대로 사용한다.

하지만 각도 변화량은 길이 변화량, 즉 호의 변화량으로 생각하여, 그 길이의 변화량을 구해야 한다.

위와 같은 그림을 그려보고, 조금 변한다는 것의 의미를 생각하면 금방 알 수 있다.

[!note]- Differential Operator{title}

\[\nabla = \left( \frac{\partial}{\partial r}, \frac{1}{r} \frac{\partial}{\partial \theta}, \frac{1}{r\sin \theta} \frac{\partial}{\partial \phi} \right)\]

[!question] \(\frac{1}{r}\), \(\frac{1}{r \sin \theta}\) 붙는건 뭐냐?{title} \(d f(r, \theta, \phi)\)를 정의하는 과정을 생각해보면 된다.

\[d f(r, \theta, \phi) = f(r+dr, \theta, \phi) - f(r, \theta, \phi) + \dots\] \[= \left( \frac{{\partial f}}{\partial r} \right)\cdot dr + \frac{1}{r} \left( \frac{{\partial f}}{\partial \theta} \right) \cdot r d\phi + \frac{1}{r\sin \theta} \left( \frac{{\partial f}}{\partial \phi} \right) \cdot r\sin \theta d\phi\] \[= \left( \frac{\partial}{\partial r}, \frac{1}{r} \frac{\partial}{\partial \theta}, \frac{1}{r\sin \theta} \frac{\partial}{\partial \phi} \right) f \cdot d \vec{r}\] \[= \nabla f \cdot d \vec{r}\]

\[\nabla \Phi = \frac{{\partial \Phi}}{\partial r} \hat{r} + \frac{1}{r} \frac{{\partial \Phi}}{\partial \theta} \hat{\theta} + \frac{1}{r\sin \theta} \frac{{\partial \Phi}}{\partial \phi} \hat{\phi}\] \[\nabla \cdot \vec{A} = \frac{1}{r^2\sin \theta} \left( \frac{\partial}{\partial r}(r^2\sin \theta)A_{r} + \frac{\partial}{\partial \theta} (r\sin \theta A_{\theta}) + \frac{\partial}{\partial \phi} (r A_{\phi}) \right)\] \[\nabla \times \vec{A} = \frac{1}{r^2\sin \theta} \begin{vmatrix} \hat{r} & r \hat{\theta} & r\sin \theta\hat{\phi}\\ \frac{\partial}{\partial r}& \frac{\partial}{\partial \theta} & \frac{\partial}{\partial \phi}\\ A_{r} & r A_{\theta} & r\sin \theta A_{\phi}\end{vmatrix}\] \[\nabla^2 \Phi = \frac{1}{r^2 \sin \theta}\left[ \frac{\partial}{\partial r} \left( r^2\sin \theta \frac{{\partial \Phi}}{\partial r}\right) + \frac{\partial}{\partial \theta} \left(\sin \theta \frac{{\partial \Phi}}{\partial \theta} \right) + \frac{\partial}{\partial \phi} \left( \frac{1}{\sin \theta} \frac{{\partial \Phi}}{\partial \phi} \right) \right]\]

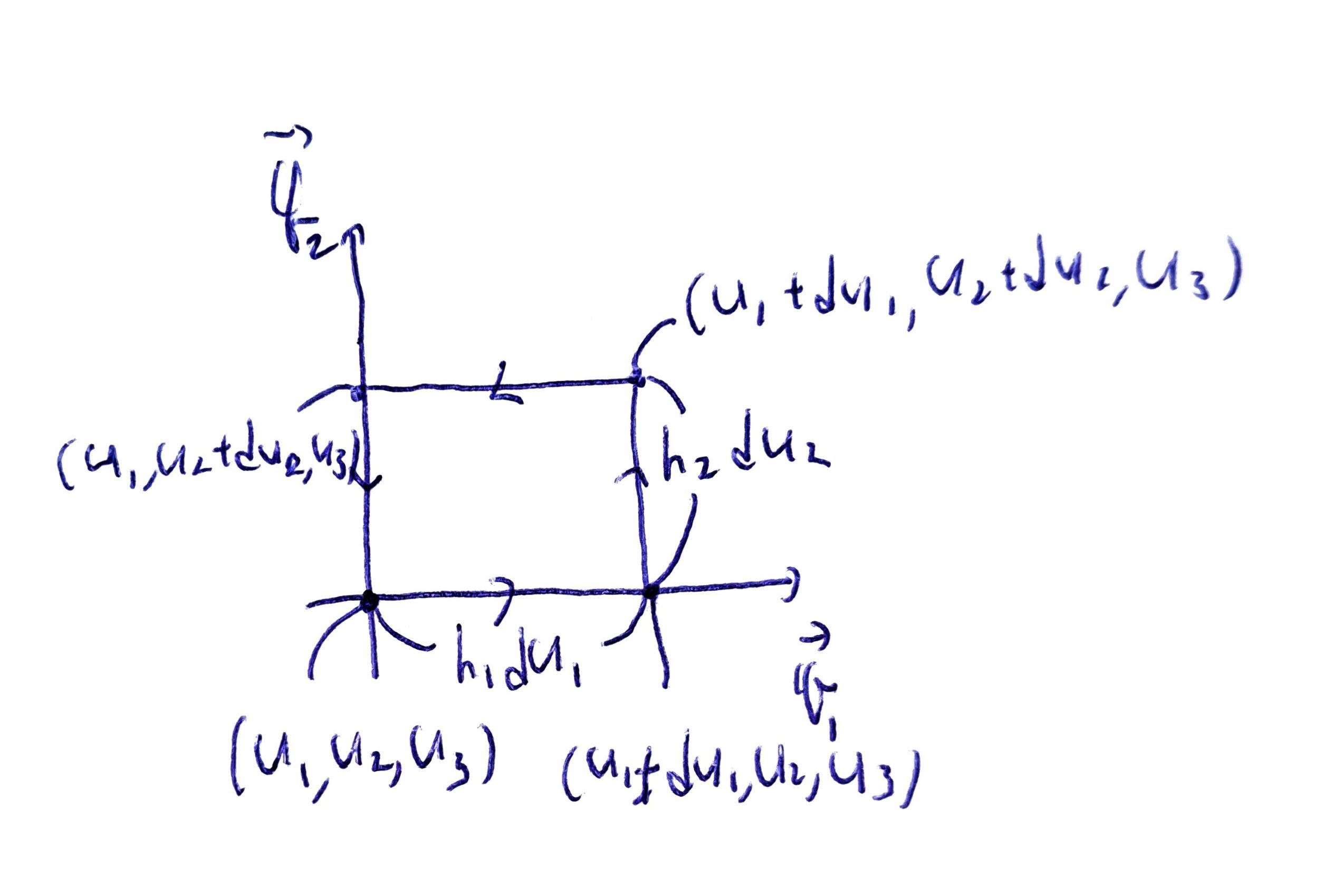
Generalized coordinate (일반화된 좌표계)

구면, 원통형 좌표계를 추상화하여 일반적으로 표기하는 방법이다. \((x, y, z)\) 대신 \((u_{1}, u_{2}, u_{3})\)을 사용하며, 단위벡터는 \(\hat{q_{1}}, \hat{q_{2}}, \hat{q_{3}}\)을 사용한다. \(d\vec{r}\)는 \(d \vec{r} = h_{1} du_{1} \hat{q}_{_{1}} + h_{2} du_{2} \hat{q_{2}} + h_{3} du_{3} \hat{q}_{3}\)와 같다. 이때 \(h_{i}\)는 \(h_{i}(u_{1}, u_{2}, u_{3})\)로 표현되는 함수를 사용한다.

• \(\displaystyle \nabla \Phi = \left( \frac{1}{h_{1}} \frac{\partial \Phi}{\partial u_{1}}, \frac{1}{h_{2}} \frac{{\partial \Phi}}{\partial u_{2}}, \frac{1}{h_{3}} \frac{{\partial \Phi}}{\partial u_{3}}\right)\)
• \(\displaystyle \nabla \cdot \vec{A} \equiv \frac{1}{h_{1}h_{2}h_{3}} \left( \frac{{\partial (h_{2}h_{3} A_{u_{1}})}}{\partial u_{1}} + \frac{{\partial( h_{1}h_{3} A_{u_{2}})}}{\partial u_{2}} + \frac{{\partial (h_{1} h_{2} A_{u_{3}})}}{\partial u_{3}}\right)\)
• \(\displaystyle \nabla \times \vec{A} = \frac{1}{h_{1}h_{2}h_{3}} \begin{vmatrix} h_{1} \hat{q}_{1} & h_{2} \hat{q}_{2} & h_{3} \hat{q}_{3}\\ \frac{\partial}{\partial u_{1}}& \frac{\partial}{\partial_{u_{2}}} & \frac{\partial}{\partial u_{3}}\\ h_{1} A_{q_{1}} & h_{2} A_{q_{2}} & h_{2} A_{q_{3}}\end{vmatrix}\)
• \(\displaystyle \nabla^2 \Phi = \frac{1}{h_{1} h_{2} h_{3}} \left[ \frac{\partial}{\partial u_{1}}\left( \frac{h_{2}h_{3}}{h_{1}} \frac{{\partial \Phi}}{\partial u_{1}} \right) + \frac{\partial}{\partial u_{2}}\left( \frac{h_{1}h_{3}}{h_{2}} \frac{{\partial \Phi}}{\partial u_{2}} \right) + \frac{\partial}{\partial u_{3}}\left( \frac{h_{1}h_{2}}{h_{3}} \frac{{\partial \Phi}}{\partial u_{3}} \right) \right]\)

	\(h_{1}\)	\(h_{2}\)	\(h_{3}\)
Cylindrical	\(1\)	\(s\)	\(1\)
Spherical	\(1\)	\(r\)	\(r\sin \theta\)

[!tip]- Gradiant 유도 과정{title}

\[d \Phi(x, y, z) = \nabla \Phi \cdot d \vec{r}\]

만약 \(\Phi\)가 \((u_{1}, u_{2}, u_{3})\)의 좌표료 표현되어 있다면 다음과 같다.

\[d \Phi (u_1, u_{2}, u_{3}) = \sum_{i=1}^{3} \frac{{\partial \Phi}}{\partial u_{i}} du_{i} = \sum_{i=1}^{3} \frac{1}{h_{i}} \frac{{\partial \Phi}}{\partial u_{i}} (h_{i} du_{i})\] \[= \left[ \frac{1}{h_{1}} \frac{{\partial \Phi}}{\partial u_{1}} \hat{q_{1}} + \frac{1}{h_{2}} \frac{{\partial \Phi}}{\partial u_{2}} \hat{q_{2}} + \frac{1}{h_{3}} \frac{{\partial \Phi}}{\partial u_{3}} \hat{q_{3}} \right] \cdot \left[ h_{1} du_{1} \hat{q}_{1} + h_{2} du_{2} \hat{q_{2} + h_{3} du_{3} \hat{q_{3}}} \right]\]

앞에 항이 \(\nabla \Phi\)와 같고, 뒤의 항이 \(d \vec{r}\)과 같다.

\[\nabla \Phi = \sum_{i} \frac{1}{h_{i}} \frac{{\partial \Phi}}{\partial u_{i}} \hat{q}_{i}\] \[\nabla \Phi = \left( \frac{1}{h_{1}} \frac{\partial \Phi}{\partial u_{1}}, \frac{1}{h_{2}} \frac{{\partial \Phi}}{\partial u_{2}}, \frac{1}{h_{3}} \frac{{\partial \Phi}}{\partial u_{3}}\right)\]

[!tip]- Divergence 유도 과정{title}

다음과 같은 Vector FIeld가 있다고 하자.

\[\vec{A}(u_{1}, u_{2}, u_{3}) = \sum_{i=1}^3 A_{i} \hat{q}_{i}\]

\(\nabla \cdot \vec{A}\)를 구하기 위해서, 발산 정리를 활용할 수 있을 것 같다.

\[\int_{V} (\nabla \cdot \vec{A})dV = \oint_{S} \vec{A} \cdot d \vec{a}\]

우리는 작은 체적을 모두 Sum하는 것은 관심 없고, 작은 체적 하나인 \((\nabla \cdot \vec{A}) dV\)만 알면 된다.

작은 체적의 \(\oint_{S} \vec{A} \cdot d \vec{a}\)를 구해보자.

1. 윗면 + 아랫면
   • \(\vec{A} \cdot d \vec{a}\) (윗면)

\[= \vec{A}(u_{1}, u_{2}, u_{3}+du_{3}) \cdot (h_{1}(u_{1},u_{2},u_{3}+du_{3}) du_{1} \cdot h_{2}(u_{1},u_{2},u_{3} + du_{3}) du_{2} \cdot \hat{q_{3}})\]

• \(\vec{A} \cdot d \vec{a}\) (아랫면)

\[= \vec{A}(u_{1}, u_{2}, u_{3}) \cdot (h_{1}(u_{1},u_{2},u_{3}) du_{1} \cdot h_{2}(u_{1},u_{2},u_{3}) du_{2} \cdot (-\hat{q_{3}}))\]

• 윗면 + 아랫면 \(\vec{A} h_{1} h_{2}\)를 하나의 함수로 생각하면,

\[\frac{\vec{A}(u_{1},u_{2},u_{3}+du_{3}) h_{1}(u_{1},u_{2},u_{3}+du_{3}) h_{2}(u_{1},u_{2},u_{3}+du_{3}) - \vec{A}(u_{1},u_{2},u_{3}) h_{1}(u_{1},u_{2},u_{3}) h_{2}(u_{1},u_{2},u_{3})}{du_{3}}du_{3}\] \[= \frac{{\partial (h_{1} h_{2} \vec{A}})}{\partial u_{3}}du_{3}\]

로 줄일 수 있다.

\[\int_{surface \bot \hat{q_{3}}} \vec{A} \cdot d \vec{a} = \frac{{\partial (h_{1} h_{2} \vec{A})}}{\partial u_{3}} \cdot du_{1} du_{2}du_{3} \hat{q_{3}}\] \[= \frac{{\partial (h_{1} h_{2} \vec{A})}}{\partial u_{3}} \frac{1}{h_{1}h_{2}h_{3}} dV \hat{q_{3}}\]

1. 왼쪽면 + 오른쪽면

똑같이 진행. 오른쪽면은 \(+du_{2}\)이므로

\[\int_{surface \bot \hat{q_{2}}} \vec{A} \cdot d \vec{a} = \frac{{\partial (h_{1} h_{3} \vec{A})}}{\partial u_{2}} \frac{1}{h_{1}h_{2}h_{3}} dV \hat{q_{2}}\]

1. 앞면 + 뒷면

\[\int_{surface \bot \hat{q_{1}}} \vec{A} \cdot d \vec{a} = \frac{{\partial (h_{2} h_{3} \vec{A})}}{\partial u_{1}} \frac{1}{h_{2}h_{2}h_{3}} dV \hat{q_{1}}\]

따라서, \(\oint_{S} \vec{A} \cdot d \vec{a}\)는 다음과 같다.

\[\oint_{S} \vec{A} \cdot d \vec{a} = \int_{surface \bot \hat{q_{1}}} \vec{A} \cdot d \vec{a} + \int_{surface \bot \hat{q_{2}}} \vec{A} \cdot d \vec{a} \int_{surface \bot \hat{q_{3}}} \vec{A} \cdot d \vec{a}\] \[= \frac{{\partial (h_{2} h_{3} \vec{A})}}{\partial u_{1}} \frac{1}{h_{2}h_{2}h_{3}} dV \hat{q_{1}} + \frac{{\partial (h_{1} h_{3} \vec{A})}}{\partial u_{2}} \frac{1}{h_{1}h_{2}h_{3}} dV \hat{q_{2}} + \frac{{\partial (h_{1} h_{2} \vec{A})}}{\partial u_{3}} \frac{1}{h_{1}h_{2}h_{3}} dV \hat{q_{3}}\] \[= \frac{1}{h_{1}h_{2}h_{3}} \left( \frac{{\partial (h_{2}h_{3} A_{u_{1}})}}{\partial u_{1}} + \frac{{\partial( h_{1}h_{3} A_{u_{2}})}}{\partial u_{2}} +\frac{{\partial (h_{1} h_{2} A_{u_{3}})}}{\partial u_{3}}\right) dV\] \[= (\nabla \cdot \vec{A}) dV\]

따라서, \(\nabla \cdot \vec{A}\)는 다음과 같다.

\[\nabla \cdot \vec{A} \equiv \frac{1}{h_{1}h_{2}h_{3}} \left( \frac{{\partial (h_{2}h_{3} A_{u_{1}})}}{\partial u_{1}} + \frac{{\partial( h_{1}h_{3} A_{u_{2}})}}{\partial u_{2}} + \frac{{\partial (h_{1} h_{2} A_{u_{3}})}}{\partial u_{3}}\right)\]

[!tip]- Curl 유도 과정{title} \(\nabla \times \vec{A}\)의 값을 알기 위해, 스토크스 정리를 사용하자.

\[\iint_{S} (\nabla \times \vec{A}) \cdot d \vec{a} = \oint_{C} \vec{A} \cdot d \vec{r}\]

우리는 딱히 전체 면적을 Sum한 결과는 관심이 없으므로, 미소 면적을 선적분해서 \((\nabla \times \vec{A}) \cdot d \vec{a}\) 값만 알아내보자.

일단, \(u_{1} u_{2}\) plane의 경우 \(d\vec{a}\)는 \(h_{1}h_{2} du_{1} du_{2} \hat{q}_{3}\)와 같다.

Right(>) Up Left(<) Down 순서대로 닫힌 Path 선적분을 해보자.

\[\int_{>} \vec{A} \cdot d \vec{r} = \int^{u_{1} + du_{1}}_{u_{1}} \vec{A}(u_{1}', u_{2}, u_{3}) \cdot h_{1}(u_{1}', u_{2}, u_{3}) \hat{q_{1}} du_{1}\] \[\int_{<} \vec{A} \cdot d \vec{r} = \int^{u_{1}}_{u_{1}+du_{1}} \vec{A}(u_{1}', u_{2} + du_{2}, u_{3}) \cdot h_{1} (u_{1}, u_{2} + du_{2}, u_{3}) \hat{q_{1}} du_{1}\] \[\int_{<} \vec{A} \cdot d \vec{r} + \int_{>} \vec{A} \cdot d \vec{r}\] \[= -\left( \int^{u_{1} + du_{1}}_{u_{1}} \vec{A}(u_{1}', u_{2} + du_{2}, u_{3}) \cdot h_{1} (u_{1}', u_{2} + du_{2}, u_{3}) \hat{q_{1}} du_{1} - \vec{A}(u_{1}', u_{2}, u_{3}) \cdot h_{1}(u_{1}', u_{2}, u_{3}) \hat{q_{1}} du_{1} \right)\] \[= - \left( \int^{u_{1} + du_{1}}_{u_{1}} \frac{{\partial ( \vec{A} (u_{1}', u_{2}, u_{3})h_{1}(u_{1}',u_{2}, u_{3}) )}}{\partial u_{2}} \cdot \hat{q_{1}} du_{2} du_{1}'\right)\]

\(\hat{q_{1}}\)이 내적되어 벡터함수인 \(\frac{{\partial ( \vec{A} (u_{1}', u_{2}, u_{3})h_{1}(u_{1}',u_{2}, u_{3}) )}}{\partial u_{2}}\)가 \(q_{1}\) 성분만 뽑혀나오게 된다. \(h_{1}\)은 스칼라 함수이므로, \(\vec{A}\)의 \(q_{1}\) 성분만 고려 가능하다.

\[= - \left( \int^{u_{1} + du_{1}}_{u_{1}} \frac{{\partial ( A_{q_{1}} (u_{1}', u_{2}, u_{3})h_{1}(u_{1}',u_{2}, u_{3}) )}}{\partial u_{2}} du_{2} du_{1}'\right)\]

\(\frac{{\partial ( \vec{A}_{q_{1}} (u_{1}', u_{2}, u_{3})h_{1}(u_{1}',u_{2}, u_{3}) )}}{\partial u_{2}}\)는 스칼라 함수이므로, 그 스칼라 함수를 \(u_{1}\)에 대해 부정적분한 함수를 \(F(u_{1}, u_{2}, u_{3})\)라고 하자.

\[F(u_{1}, u_2, u_{3}) = \int \frac{{\partial ( A_{q_{1}} (u_{1}, u_{2}, u_{3})h_{1}(u_{1},u_{2}, u_{3}) )}}{\partial u_{2}} du_{1}\] \[= - (F(u_{1} + du_{1}, u_{2}, u_{3}) - F(u_{1}, u_{2}, u_{3})) du_{2}\] \[= - \frac{F(u_{1} + du_{1}, u_{2}, u_{3}) - F(u_{1}, u_{2}, u_{3})}{du_{1}} du_{1} du_{2}\] \[= - \frac{{\partial F(u_{1}, u_{2}, u_{3})}}{\partial u_{1}} du_{1} du_{2}\]

\(F(u_{1}, u_{2}, u_{3})\)을 \(u_{1}\)에 대해 미분하면 다시 원함수가 나온다.

\[= - \frac{{\partial ( h_{1}A_{q_{1}} )}}{\partial u_{2}} du_{1}du_{2}\]

똑같이 위 아래도 선적분하면 다음과 같다.

\[\frac{{\partial ( h_{2}A_{q_{2}} )}}{\partial u_{1}} du_{1}du_{2}\]

두개를 더하면

\[\left[ \frac{{\partial ( h_{2}A_{q_{2}} )}}{\partial u_{1}} - \frac{{\partial ( h_{1}A_{q_{1}} )}}{\partial u_{2}} \right] du_{1}du_{2}\] \[= \frac{1}{h_{1}h_{2}} \left[ \frac{{\partial ( h_{2}A_{q_{2}} )}}{\partial u_{1}} - \frac{{\partial ( h_{1}A_{q_{1}} )}}{\partial u_{2}} \right] \hat{q}_{3} = (\nabla \times \vec{A})_{q_{3}}\]

나머지 \(\nabla \times \vec{A}\)의 \(q_{1}\), \(q_{2}\) 성분을 똑같은 방법으로 구할 수 있다.

\[(\nabla \times \vec{A})_{q_{1}} = \frac{1}{h_{2}h_{3}} \left[ \frac{{\partial ( h_{3}A_{q_{3}} )}}{\partial u_{2}} - \frac{{\partial ( h_{2}A_{q_{2}} )}}{\partial u_{3}} \right]\] \[(\nabla \times \vec{A})_{q_{3}} = \frac{1}{h_{3}h_{1}} \left[ \frac{{\partial ( h_{1}A_{q_{1}} )}}{\partial u_{3}} - \frac{{\partial ( h_{3}A_{q_{3}} )}}{\partial u_{1}} \right]\] \[(\nabla \times \vec{A})_{q_{3}} = \frac{1}{h_{1}h_{2}} \left[ \frac{{\partial ( h_{2}A_{q_{2}} )}}{\partial u_{1}} - \frac{{\partial ( h_{1}A_{q_{1}} )}}{\partial u_{2}} \right]\]

이를 행렬식으로 표현하면 다음과 같다.

\[\nabla \times \vec{A} = \begin{vmatrix} \frac{1}{h_{2}h_{3}} \hat{q}_{1} & \frac{1}{h_{1}h_{3}} \hat{q}_{2} & \frac{1}{h_{1}h_{2}} \hat{q}_{3}\\ \frac{\partial}{\partial u_{1}}& \frac{\partial}{\partial_{u_{2}}} & \frac{\partial}{\partial u_{3}}\\ h_{1} A_{q_{1}} & h_{2} A_{q_{2}} & h_{2} A_{q_{3}}\end{vmatrix}\] \[= \frac{1}{h_{1}h_{2}h_{3}} \begin{vmatrix} h_{1} \hat{q}_{1} & h_{2} \hat{q}_{2} & h_{3} \hat{q}_{3}\\ \frac{\partial}{\partial u_{1}}& \frac{\partial}{\partial_{u_{2}}} & \frac{\partial}{\partial u_{3}}\\ h_{1} A_{q_{1}} & h_{2} A_{q_{2}} & h_{2} A_{q_{3}}\end{vmatrix}\]

[!tip]- Laplacian 유도 과정{title}

\[\nabla^2 \Phi = \nabla \cdot \nabla \Phi\] \[= \nabla \cdot \left( \frac{1}{h_{1}} \frac{{\partial \Phi}}{\partial u_{1}}, \frac{1}{h_{2}} \frac{{\partial \Phi}}{\partial u_{2}}, \frac{1}{h_{3}} \frac{{\partial \Phi}}{\partial u_{3}} \right)\] \[= \frac{1}{h_{1} h_{2} h_{3}} \left[ \frac{\partial}{\partial u_{1}}\left( \frac{h_{2}h_{3}}{h_{1}} \frac{{\partial \Phi}}{\partial u_{1}} \right) + \frac{\partial}{\partial u_{2}}\left( \frac{h_{1}h_{3}}{h_{2}} \frac{{\partial \Phi}}{\partial u_{2}} \right) + \frac{\partial}{\partial u_{3}}\left( \frac{h_{1}h_{2}}{h_{3}} \frac{{\partial \Phi}}{\partial u_{3}} \right) \right]\]