고급컴퓨터그래픽스 6. Hierarchical Animation

건국대학교 고급컴퓨터그래픽스 김형석 교수님의 수업을 정리한 내용입니다.

Hierarchical Object

단순한 object가 아니라, 복잡한 연결 관계를 가진 object는 부속 부품들의 Parent-Child 관계를 정하고, Parent가 움직이면 Child가 따라 움직이는 방식으로 애니메이션 할 수 있다. 이는 사람, 로봇, 동물, 자동차, … 등 모든 복잡한 구조를 가진 object에 적용 가능하다.

Parent-Child 구조를 저장하기 위해 Tree를 사용한다.

• Link : object의 component. 관절과 관절 사이를 연결하므로 Link라고 부른다.
• Joint : 관절. 각 관절은 상대적인 움직임을 가질 수 있으며, 움직임 Limit와 자유도를 갖는다.
• End Effector : object가 작업을 하는 가장 마지막 component. 사람의 경우 발, 손이 이에 해당함.
• Pose Vector : 모든 Joint 각도의 집합

Forward Kinematics (FK)

직접 관절의 움직임을 설정해서 애니메이션을 만드는 방법이 FK 방식이다. 구현은 간단하지만, 이것 만으론 무리가 있다.

Joint는 회전하는 Joint, 늘어나거나 줄어드는 Joint 두가지 타입이 존재한다.

Inverse Kinematics (IK)

만약 컵에 손을 뻗는 동작을 만들고 싶다면 손을 컵쪽으로 옮기기만 하면 알아서 손목, 팔, 어깨 관절의 각도를 계산해주면 편하지 않을까? 이것이 IK 방식이다. End Effector의 위치를 설정하면, Tree의 아래에서 위로 올라가면서 자동으로 관절을 계산해주도록 한다.

IK의 부모 관절 각도를 계산하기 위해 해석적인 방법과 수치적인 방법이 존재한다.

[!question]- Analytic Solution?{title}

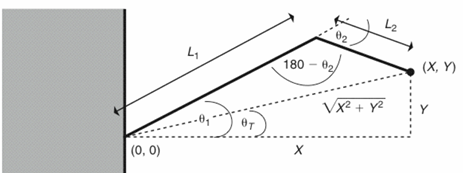
2개의 팔과 2개의 관절(어깨, 팔꿈치 부위)만 갖는 단순한 로봇 팔의 경우 해석적 Solution이 존재한다. 루트 노드를 원점으로 하고, End Effector의 목표 지점을 \((x,y)\), 각각의 팔 길이를 \(l_{1}, l_{2}\), \(d=\sqrt{ x^2+y^2 }\), 첫번째 관절 각도와 두번째 관절 각도를 \(\theta_{1}, \theta_{2}\)라고 하자. 구해야 하는 값은 바로 \(\theta_{1}, \theta_{2}\) 값이다. 다음과 같은 Solution이 존재한다.

\[\displaystyle \theta_{2}= \cos^{-1}\left(- \frac{l_{1}^2 + l_{2}^2 - d^2}{2 l_{1} l_{2}} \right)\] \[\displaystyle \theta_{1} =\cos^{-1}\left( \frac{l_{1}^2 - l_{2}^2 + d^2}{2l_{1}d} \right) + \theta_{T}\] \[\displaystyle \theta_{T} = \cos^{-1}\left( \frac{x}{d} \right)\]

Numeric Solution? : Jacobian

\(X=[x,y,z]\), \(\theta=[\theta_{1},\theta_{2},\dots,\theta_{n}]\)이라고 하자. \(\Delta X\)를 통해 \(\Delta \theta\)를 구해내고 싶다. 두 변화량은 어떤 변환 행렬로 연결되어 있으며, 그 행렬은 자코비안이다.

\[\Delta X=J\Delta \theta\] \[J=\left[ \begin{matrix} \frac{{\partial x}}{\partial \theta_{1}} & \frac{{\partial x}}{\partial \theta_{2}} & \dots \\ \frac{{\partial y}}{\partial \theta_{1}} & \frac{{\partial y}}{\partial \theta_{2}} & \dots \\ \frac{{\partial z}}{\partial \theta_{1}} & \frac{{\partial z}}{\partial \theta_{2}} & \dots \end{matrix} \right]\]

따라서 \(\Delta \theta=J^{-1} \Delta X\)로 관절 값을 알아낼 수 있다. 하지만 자코비안의 역을 계산할 수 없을 경우, \(\Delta \theta = J^+ \Delta X\) 수도 역행렬을 사용한다.

\[(J^T J)^{-1} J^T = J^+\]

자코비안이 어떤 특이점을 가지면 무한대의 값이 가끔 나온다. 이를 해결하기 위해 감쇠 요소를 추가하여 해결한다.

\[\Delta \theta = (J^TJ + \lambda^2 I)^{-1}J^T \Delta X\]

Numeric Solution? : Cyclic Coordinate Descent (CCD)

관절을 Bottom-Up 방식으로 따로따로 계산하여 점진적으로 End Effector가 목표 위치에 도달할 수 있도록 반복하여 계산하는 방법이다.