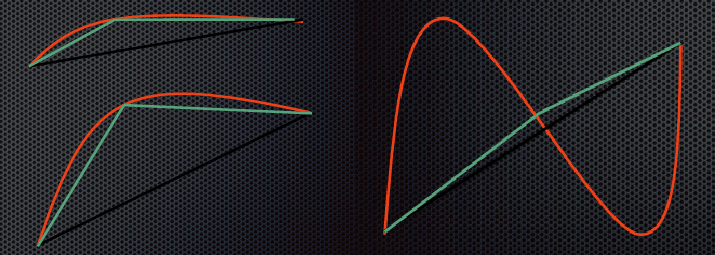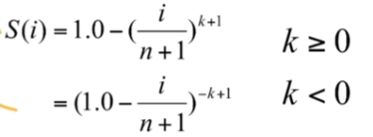고급컴퓨터그래픽스 5. Interpolation-based Animation
건국대학교 고급컴퓨터그래픽스 김형석 교수님의 수업을 정리한 내용입니다.
Computer Animation Methods
- Physic Simulation
- Good 퀄리티
- Many 계산량
- Keyframe
- Simple
- 아티스트에 따라 퀄리티 달라짐
- Motion Capture
- 키프레임을 기계가 잡아줌
- 모델에 따라 키프레임을 다시 맞춰줘야 함
How to Animation?
object의 시간에 따라 property value의 값을 설정해두고, 그 값을 Spline으로 보간하면 된다. property value를 \(p\)라고 하면, \(p=P(L^{-1}(S(t)))\) 함수를 사용하여 시간을 매개변수로 하는 보간 Spline을 얻을 수 있다.
[!question]- What is \(p=P(L^{-1}(S(t)))\)?{title} Key는 \((\text{time}, \text{position})\) 쌍의 집합으로 주어져야 자연스럽다. 주어진 Key를 반드시 지나도록 중간 경로를 자연스럽게 생성해야 한다.
최종 위치를 \(p\)라고 하자. 위치 값이므로, \(p\)는 2차원 또는 3차원 벡터가 되어야 할 것이다. 주어진 Key의 시간 집합을 \(\{t_{0}, t_{1}, \dots, t_{n}\}\), 위치 집합을 \(\{ p_{0}, p_{2}, \dots, p_{n} \}\)라고 하자. 보간 곡선은 \(u=[0,1]\) 범위의 파라미터를 사용하는 \(p=P(u)\) 함수를 사용할 수 있다. 하지만 파라미터 \(u\)는 직관적이지 않으므로, 곡선의 길이 함수 \(\displaystyle s=L(u)=\int_{u_{0}^{u}} \lvert P'(u') \rvert du'\)의 역함수인 \(u=L^{-1}(s)\)를 사용하여 \(p=P(L^{-1}(s))\)로 바꾼다. 길이를 파라미터로 쓰는 것보단, 시간을 파라미터로 쓰는게 가장 좋으므로 \(s=S(t)\) 함수를 도입하여 최종적으로 \(p=P(L^{-1}(S(t)))\) 시간을 입력으로 받아 Key Set을 자연스럽게 지나는 보간 함수를 완성한다.
[!tip]- \(p=P(u)\) 함수 종류 (Spline){title}
- Spline Interpolation
- Linear Spline
- Bezier Spline
- Hermite Spline
- Catmull-Rom Spline
- B-Spline
- Lagrange Polynomial Interpolation : \(\displaystyle P(u) = \sum_{j=0}^{k}y_{i} \prod_{0\leq m<k, m\neq i} \frac{{x-x_{m}}}{x_{i}-x_{m}}\)
- \(p_{i}=(x_{i},y_{i})\), \(\displaystyle \prod_{0\leq m<k, m\neq i}\) : \(0\leq m<k, m\neq i\) 조건의 값을 모두 곱하라.
- Key가 많아질수록 오류가 커진다.
[!tip]- \(u=L^{-1}(s)\) 계산 방법 (Super Sampling){title} \(u=L^{-1}(s)\) 함수를 컴퓨터로 해석적으로 적분하고, 역함수를 구하는 것은 힘드므로 수치해석 방법으로 접근한다. \(\displaystyle \int_{u_{0}^{u}} \lvert P'(u') \rvert du' \simeq \sum_{i=0}^\text{res} \lvert P(u_{i}) -P(u_{i-1}) \rvert\), \(\text{res} =\) 해상도, 얼마나 잘게 쪼갤 거냐를 의미한다. 예를들어, \(res=20\)으로 설정 후 값을 계산하면 하나의 Table을 만들 수 있다. 테이블은 DP로 구현할 수 있을 듯.
index u s 0 0 0.000 1 0.05 0.08 2 0.10 0.15 3 0.15 0.23 … … … 20 (res) 1.00 1.00 이후 \(s=0.10\)일 때 대응하는 u를 찾고 싶다면, table에서 Binary Search하여 0.1과 가장 근접한 두 \(s\)값을 찾는다. 또는 Table을 Binary Tree로 구현해서 successor와 predecessor를 찾으면 된다. 이를 \(s_{k}, s_{k+1}\)이라고 하자. \(s, s_{k}, s_{k+1}\)의 비율을 계산하여 그 비율만큼 \(u_{k}, u_{k+1}\) 에 곱해주면 원하는 \(u\)값을 찾을 수 있다. \(\displaystyle u= \frac{s_{k+1}-s}{s_{k+1}-s_{k}}(u_{k+1}-u_{k}) + u_{k}\), 이 방식을 Super Sampling라고 한다.
이후 적절한 해상도 값 \(res\)를 어떻게 찾을 수 있을까? \(res\) 값을 점점 늘려가면서 총 곡선 길이의 차이가 크지 않을때까지 \(res\)를 늘려가면 된다. 체크는 1번에 끝내는게 아니라, 2~3번 해줘야 한다. 그 이유는 오른쪽 그림과 같은 예외 케이스가 존재하기 떄문이다.
[!tip]- \(s=S(t)\) 함수 종류{title}
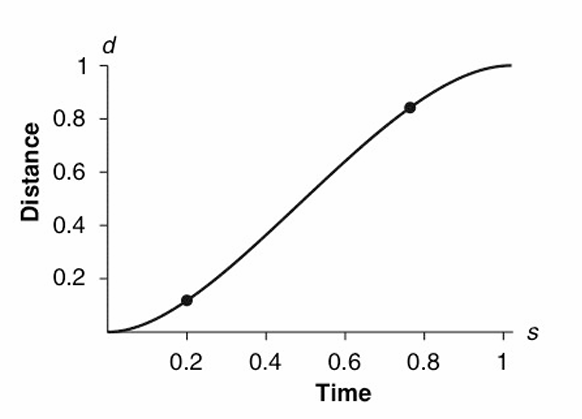
일반적으로 Ease-in/Ease-out Function 함수를 사용해서 부드럽게 이동할 수 있도록 한다.
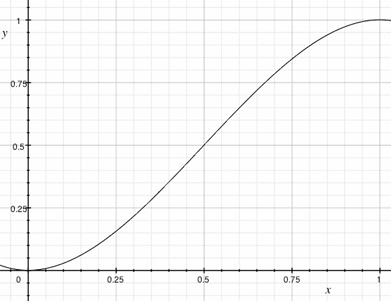
\[S(t)= \frac{1}{2} \left( \sin\left( t \pi-\frac{\pi}{2} \right) +1 \right)\]
- Sinusoidal
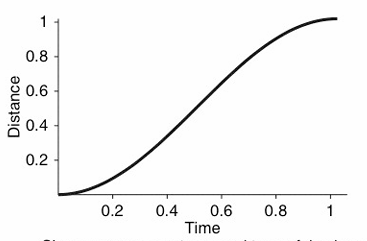
\[S(t) = -2t^3+3t^2\]
- Single Cubic
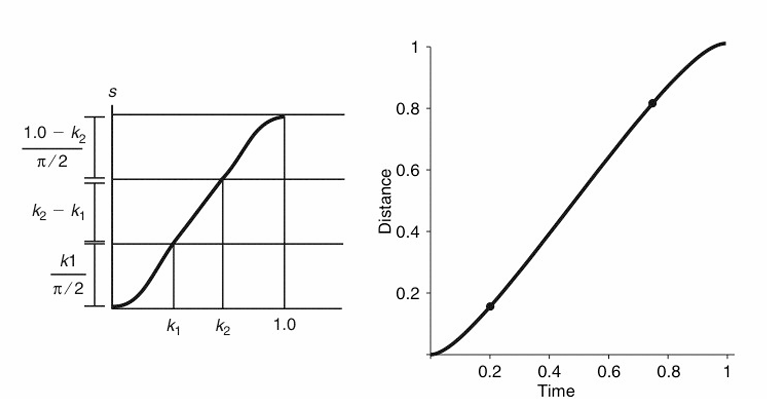
\[S(t) = \begin{cases} \frac{1}{f} \cdot{k_1 \frac{2}{\pi} \left(\sin\left(\frac{t \pi}{2 k_1} - \frac{\pi}{2}\right)\right)} & t \leq k_1 \\[10pt] \frac{1}{f}\left( {\frac{k_1}{\frac{\pi}{2}} + (t - k_1)} \right) & k_1 < t \leq k_2 \\[10pt] \frac{1}{f} \left( {\frac{k_1}{\frac{\pi}{2}} + k_2 - k_1 + (1 - k_2) \frac{2}{\pi} \sin\left(\frac{\pi (t - k_2)}{2 (1 - k_2)}\right)} \right) & t > k_2 \end{cases}\] \[\displaystyle f = k_1 \frac{2}{\pi} + k_2 - k_1 + (1 - k_2) \frac{2}{\pi}\]
- Piecewise Sinusoidal
\[\displaystyle S(t) = \begin{cases} \frac{v_0 t^2}{2 t_1} & 0.0 < t \leq t_1 \\[10pt] v_0 \frac{t_1}{2} + v_0 (t - t_1) & t_1 < t \leq t_2 \\[10pt] v_0 \frac{t_1}{2} + v_0 (t_2 - t_1) + v_0 \left(1 - \frac{(t - t_2)}{2 (1 - t_2)}\right)(t - t_2) & t_2 < t \leq 1.0 \end{cases}\]
- Constant Acceleration
\(t_{1}, t_{2}\)는 각각 가속이 끝나는 시간, 가속이 시작되는 시간으로 임의로 설정 가능하다.
[!tip]- 그래프 모양, 순서대로 1. 2. 3. 4.{title}
Rotate Animation
- 수동 Animating : object의 euler angle property를 정의하고, x, y, z 각도를 직접 animating 할 수 있다.
- 자동 Animating : 만약 객체가 움직이는 경로를 보고 항상 앞을 바라보게 하고 싶다면, Path의 접선, 법선 벡터를 구해서 Forward, Up 방향으로 지정한다. 이후 벡터를 보간하기 위해 Quaternion Interpolation을 사용한다.
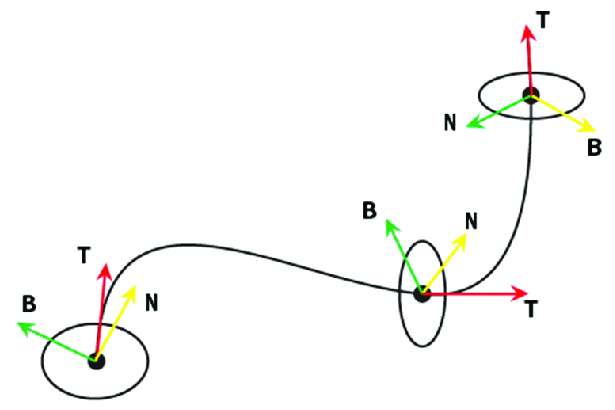
[!tip]- Tangent Vector, Normal Vector 구하는 법{title}
오브젝트는 위치 뿐만이 아니라 방향 정보도 가져야 한다. 나의 위치, 바라보는 방향, 위의 방향을 모두 포함하는 좌표계를 사용하는데, 이를 Frenet Frame라고 한다. \(P(t)\)를 알고 있으면, 앞, 위, 옆 방향을 모두 자동으로 계산해낼 수 있다.
- \(T\)는 Tangent Vector로 곡선의 접선 방향, 즉 앞 방향과 같다. \(\displaystyle T(u) = \frac{P'(u)}{\lvert P'(u) \rvert}\)
- \(N\)은 Normal Vector로 곡선의 법선 방향, 즉 위 방향과 같다. \(\displaystyle N(u)= \frac{T'(u)}{\lvert T'(u) \rvert} = \frac{P''(u)}{\lvert P''(u) \rvert}\)
- \(B\)는 Binormal로 두 곡선의 Cross 곱, 즉 옆 방향과 같다. \(\displaystyle B(u) = T(u) \times N(u)\)
따라서 \(P'(u)\)와 \(P''(u)\)를 구할 수 있다면 바라보는 방향을 자동으로 계산할 수 있다.
\(P(u) = UMB\)일 때 \(P'(u)=U'MB\), \(P''(u)=U''MB\)이다. \(U= \left[ \begin{matrix} u^3 & u^2 & u & 1 \end{matrix} \right]\), \(U'= \left[ \begin{matrix} 3u^2 & 2u & 1 & 0 \end{matrix} \right]\), \(U''= \left[ \begin{matrix} 6u & 2 & 0 & 0 \end{matrix} \right]\)이므로 \(u=L^{-1}S(t)\) 를 통해 u값을 계산해서 행렬곱 계산만 하면 해당 점에서 \(T, N ,B\) 벡터를 계산할 수 있다.
[!tip]- Vector를 보간하는 법 : Quaternion Interpolation{title} \(T, N,B\) 벡터를 쌩으로 보간하는 것은 어렵고, 보간을 해도 결과가 이상하다. 따라서 \(T, N, B\) 벡터를 \(R= \left[ \begin{matrix} T_{x} & N_{x} & B_{x} \\ T_{y} & N_{y} & B_{y} \\ T_{z} & N_{z} & B_{z} \end{matrix} \right]\)의 회전 행렬로 표현하고, 회전 행렬을 쿼터니언으로 바꿔서 두 쿼터니언 사이를 보간 후, 보간된 쿼터니언을 다시 회전 행렬로 변환하는 아이디어를 사용한다.
각 Sample된 점마다 \(T, N, B\) 벡터를 행렬로 바꾸고, 행렬을 쿼터니언으로 변환한다. 이후 쿼터니언을 보간하기 위해 Sin Linear (Slerp) Interpolation 또는 Bazier Spline Interpolation 방법을 사용한다.
[!question]- Quaternion?{title}
복소수는 실수 체계의 2차원 확장이고, \(z=a+bi\)와 같다. 쿼터니언은 실수 체계의 4차원 확장이고, \(q=s+x i + y j + z k\)와 같다. \(i, j, k\)는 각각 다른 방향의 허수 차원이며, \(i^2 = j^2 = k^2 = ijk = -1\)가 성립한다. 편의상 \(q=s+x i + y j + z k\)와 같은 쿼터니언을 \(\vec{v}=(x,y,z)\) 벡터로 생각하여 \(q=[\begin{matrix}s & \vec{v}\end{matrix}]\)로 표기할 수 있다.
쿼터니언의 기본 연산은 다음과 같다.
- Addition : \(q_{1} +q_{2} = [\begin{matrix} s_{1} + s_{2} & \vec{v}_{1} + \vec{v}_{2} \end{matrix}]\)
- Multiplication : \(q_{1}q_{2} = [\begin{matrix} s_{1}s_{2} - \vec{v}_{1} \cdot \vec{v}_{2} &s_{2}\vec{v}_{1} + s_{1}\vec{v}_{2} + \vec{v}_{1} \times \vec{v}_{2} \end{matrix}]\)
- Inner Product : \(q_{1} \cdot q_{2} = s_{1}s_{2} + v_{1} \cdot v_{2}\)
- Length : \(\lvert \lvert q \rvert \rvert = \sqrt{ q \cdot q }\)
- Inverse : \(\displaystyle q^{-1} = \frac{1}{\lvert \lvert q \rvert \rvert^2} [ \begin{matrix}s & -\vec{v}\end{matrix}]\)
- Unit quaternion : \(\displaystyle\hat{q} = \frac{q}{\lvert \lvert q \rvert \rvert}\)
각종 변환 공식은 다음과 같다. 1) Axis, \(\theta\) \(\to\) Quaternion : \(\displaystyle q = \cos\left( \frac{\theta}{2} \right) + \sin\left( \frac{\theta}{2} \right)(x i + yj + z k) = \left[ \begin{matrix} \cos \left( \frac{\theta}{2} \right) & \sin \left( \frac{\theta}{2} \right) \vec{v} \end{matrix} \right]\) - 이때 축을 \(\lvert (x,y,z) \rvert=1\)을 사용하여 Unit Quaternion으로 만드는게 좋다.
3) Quaternion \(\to\) Axis, \(\theta\) - $$\theta = 2 \cos^{-1}(s)\(- \\)\displaystyle(x,y,z) = \frac{\vec{v}}{\lvert \vec{v} \rvert}$$
4) 회전 변환 행렬 \(R \to\) Quaternion
5) Quaternion -> 회전 변환 행렬 \(R = \begin{bmatrix}1 - 2y^2 - 2z^2 & 2xy - 2sz & 2xz + 2sy \\2xy + 2sz & 1 - 2x^2 - 2z^2 & 2yz - 2sx \\2xz - 2sy & 2yz + 2sx & 1 - 2x^2 - 2y^2\end{bmatrix}\)
6) Vector -> Quaternion : \(\vec{v}=(v_{x},v_{y},v_{z}) \to q_{v}\implies q_{v} = 0 + v_{x}i + v_{y}j + v_{z}k\)
7) Quaternion -> Vector : \(q_{v}' = 0 + v_{x}'i + v_{y}'j + v_{z}'j \implies \vec{v}'=(v_{x}', v_{y}', v_{z}')\)
8) 어떤 벡터 \(\vec{v}=(v_{x}, v_{y}, v_{z})\)를 쿼터니언으로 회전시키고 싶다면 다음 과정을 거치면 된다. 1. 벡터를 쿼터니언으로 변환. 2. 벡터를 회전. \(q_{v}' = q \cdot q_{v} \cdot q^{-1}\) 3. 회전된 쿼터니언을 다시 벡터로 변환.
[!question]- Lerp?{title} Lerp는 선형 보간을 의미한다. 함수로 표현하면 다음과 같다. \(\text{lerp}( P_{0}, P_{1}, t ) = (1-t)P_{0} + tP_{1}\)
lerp는 선형 보간을 의미한다. 만약 쿼터니언을 선형 보간하면, 구간이 일정하지 않다는 문제가 발생한다. 따라서 각도에 따라 선형 보간을 하면 되는데, 그 방법을 Slearp라고 한다.
\[\displaystyle \text{slerp}(q_{1}, q_{2}, u) = \frac{\sin((1-u)\theta)}{\sin \theta}q_{1} + \frac{\sin(u\theta)}{\sin \theta}q_{2}\]
[!error]- 보간할 때 주의사항 : Dual representation{title}
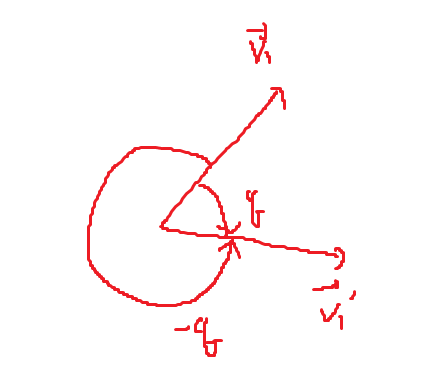
쿼터니언은 회전을 나타낸다. \(q\). 그런데 \(q\)와 \(-q\)는 동일한 회전 결과를 표현하고, 회전하는 방향이 다를 뿐이다. 따라서 두 쿼터니언의 회전 \(\theta\) 중 작은 쿼터니언을 선택해야 자연스러울 것이다.
우리는 두 쿼터니언 \(q_{1}\), \(q_{2}\) 사이의 보간을 보고 있다. \(q_{1}\)에서 \(q_{2}\)로 갈거냐, \(-q_{2}\)로 갈거냐를 선택해야 한다. 방법은 두 쿼터니언을이 Unit Quaternion이면, 두 쿼터니언을 내적한 결과가 두 쿼터니언 사이의 \(\cos \theta\)값이 된다. 따라서 \(q_{1} \cdot q_{2}\)와 \(q_{1} \cdot (-q_{2})\) 결과 중 큰 값을 고르면 더 작은 \(\theta\) 값을 고를 수 있다.
[!question]- Bezier Spline?{title} \([q_{1}, q_{2}, \dots, q_{n}]\) 쿼터니언을 보간하기 위해 Spline을 사용할 수 있다. Bezier Spline을 사용하면, De Casteljau 알고리즘을 사용할 수 있다.
De Casteljau 알고리즘의 아이디어는 나눌 수 없을 때까지 재귀적으로 Lerp하는 것이다. 현재 Quaternion을 보간하고 싶으므로 Lerp 함수 대신 Slerp 함수를 사용하면 된다. 쉐이더에서 구현한다고 하면 재귀 대신 DP를 사용하면 될 듯. \(q_{i,j}(u) = Slerp(q_{i,j-1}, q_{i+1,j-1},u)\) \(q_{0,1}, q_{1, 1}, q_{2,1} \to q_{0, 2}, q_{1, 2} \to q_{0,3}\) 순서대로 계산해서 최종적으로 \(q_{0,3}(u)\)이 원하는 Bezier Spline 곡선 함수가 되겠다.
Smoothing data
입력된 데이터 중 급격한 변화, 노이즈를 줄여야할 때가 있다. 예를들어 모션캡쳐 후 생성된 Key를 바로 사용하는 것보다, 한번 Smoothing 과정을 거치고 사용하면 훨씬 자연스럽다.
아이디어는, 각 점마다 주변 값과의 비율을 계산해 평균을 내는 것이다. Data Set을 \([P_{1}, P_{2}, \dots, P_{n}]\)이라고 할 때, 모든 점 \(\begin{matrix}P_{i}~ (\text{for } 1 \leq i \leq n)\end{matrix}\)마다 한번씩 다음과 같은 과정을 거친다.
- 필터와 범위를 선택한다.
- 나 포함 주변 값의 Value * 가중치를 곱해 전부 더한다. \(\displaystyle \sum_{k=i-\frac{R}{2}}^{k+R/2} P_{k} w_{k}\) 범위 만큼의 주변값을 확인한다.
- Sum한 값의 가중치의 합으로 나눠 정규화한 값으로 원래 값을 대체한다. \(\displaystyle P_{i}' =\frac{\text{Sum}}{\sum_{k}w_{k}}\)
Keyframe
오브젝트의 Property 값을 시간에 따라 값을 설정하고, 그 중간값은 보간하여 애니메이션을 하는 기법.
Animation Language
특정 frame (시간)의 object의 property를 language 형태로 지정하면 편할 것 같다. 이를 위한 여러 Animation Language가 존재한다.
- Artist-oriented animation language
- set position A (20, 30, 32) at frame 328
- change rotation B (1,1,0) by 45 from frame 328 to 350
- 위와 같이 스크립트를 짜서, 모든 것을 아티스트가 만드는 방법이다.
- 간단하지만, 만약 1000개의 Vertex를 애니메이팅해야할 경우 너무 힘들다.
- Full-featured programming languages for animation
- C 스타일로 애니메이션 스크립트를 짤 수 있고, Maya에서 이 방식을 사용한다.
- 한 점이 움직이면, 다른 점이 그 점을 따라서 움직이게 만들 수 있다.
- 또는 다양한 동적 조건들을 설정할 수 있다.
- Graphical Languages
- 시간-위치 그래프, 시간-속도 그래프로 키프레임을 찍는 방법.
- 애니메이터가 가장 많이 사용하는 방법이다.
Deformable Animation
피부의 탄력, 털, 옷, 표정과 같은 애니메이션을 주려면 object 모양 자체가 바뀌어야 한다.
- Vertex 자체를 직접 조작하는 방법이 있다.
(Vertex Manipulation) - Vertex를 전부 다 다루지 말고, 특징점만 움직이고 나머지 점은 그 특징점을 따라오도록 하자.
(Vertex warping) - object의 Surface를 2D Grid 안에 포함시키고, Grid의 Control Point를 조작하면 주변 점들이 따라오도록 하자.
(2D grid-based deforming) - object 내의 뼈대를 정의해서, 뼈대를 조작하면 주변 점이 따라오도록 하자.
(2D skeleton-based bending) - object를 3D Grid 안에 포함시키고, Grid의 Control Point를 조작하면 주변 점들이 따라오도록 하자.
(FFD (Free-Form Deformation))
[!question]- Vertex Warping?{title}
- Vertex를 하나 하나 직접 다루는 것은 무지 힘들기 때문에, 점을 움직이면 주변 점이 따라오도록 하는게 좋다.
- 움직이는 점을 어떤 점들이 따라가야할지 정해야 한다. 보통 인접한 곳에서 거리 \(D\)만큼 떨어진 점들이 따라 움직이도록 한다. 또, 멀리 떨어진 점일수록 덜 움직이고, 가까이 붙은 점일수록 많이 따라오도록 한다.
- 많이 사용하는 Power Curve는 다음과 같다.
- 모양이 어떻게 변할지 사사용자 지정하기가 어렵다. 점을 안으로 집어넣으면 주변 점이 튀어오른다던가 하는 효과 구현을 하기 어렵다.
[!question]- 2D Grid-based deforming?{title} object의 Surface를 포함하는 2D Grid를 정의하고, Grid의 Control Point를 조작한다. 보간 방법은 Inverse bilinear mapping라는 선형 보간 기법을 사용한다. 이건 2D 평면의 4개의 꼭짓점을 기준으로 정의된 좌표를 다른 공간으로 변환할 때 사용 가능한 기법이다.
공간을 변화시키는 것은 행렬로 표현 가능하다. \(p' = M(p)p\)
[!question]- 2D Skeleton-based Bending?{title} 스켈레톤을 정의하고, 스켈레톤을 움직임으로써 점이 따라 움직이도록 구현하는 방법.
[!question]- Free-Form Deformation?{title} object의 Bounding Box를 만든다. 이후 uniform하게 Bounding Box를 잘라 Grid를 생성한다. 그 좌표를 \((s, t, u)\)라고 하자. 각 격자점을 Control Point로 생각할 수 있다. 3중 Bezier Spline을 생성하면 가능하다. Control Point를 옮기면, Control Point 주변의 Vertex가 그 Control Point를 적절하게 따라서 움직이면 object의 모양을 변화시킬 수가 있다.
Facial Animation (안면), Sknning에서 이 방법을 사용한다.
Object Interpolation
모양이 완전히 다른 두 Object를 보간할 수 있을까? 예를들어 구에서 원뿔 모양으로 객체를 바꾸고 싶다면, Source Object와 Target Object 사이의 Vertex Correspondence를 찾아내는 것이 가장 중요하다. Correspondence란 대응 관계를 의미한다. 다음과 같은 Methods가 존재한다.
- Case of matching topology
- Radial mapping : 두 물체의 Topology (위상적 모양)이 비슷한 경우 사용 가능한 방법.
- Case of mapping on sphere
- Map to sphere
- Case of Difficult
- Object subdivision : Vertex의 개수가 작은 쪽을 계속 나눠서 개수가 같아질 때까지 나눈다. 이후 가까운 점끼리 mapping한다.
- Map the boundarie : 도형을 Convex Hull해서 Boundry를 찾는다. 이후 Boundry의 Vertex를 딱 하나를 Mapping하고, 그 Vertex를 기준으로 거리를 계산해서 거리 비율대로 가장 근처의 점을 Mapping한다.
[!question]- Radial mapping?{title} 두 Object의 Center of mess 또는 Central Axis가 내부에 있고, 두 Object 모양을 겹쳤을 때 생기는 영역(kernel)이 Simple Connected하다면 사용 가능하다.
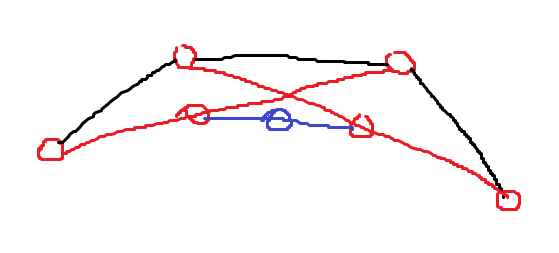
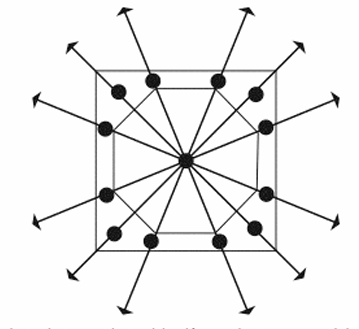
중심점에서부터 Ray를 방사한다. 이후 Ray의 두 교점의 Vertex끼리 서로 Correspondence 관계를 맺으면 된다. Correspondence 관계를 찾으면 보간은 간단해진다.
[!question]- Map to sphere?{title} 두 물체의 체적이 Simply Connected해서 두 object의 mesh를 감싸는 Sphere에 전부 mapping이 가능한 경우 사용 가능한 방법이다.
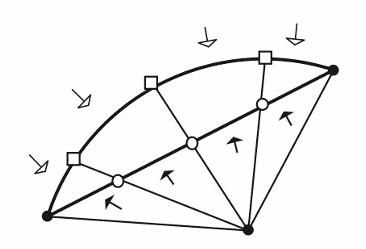
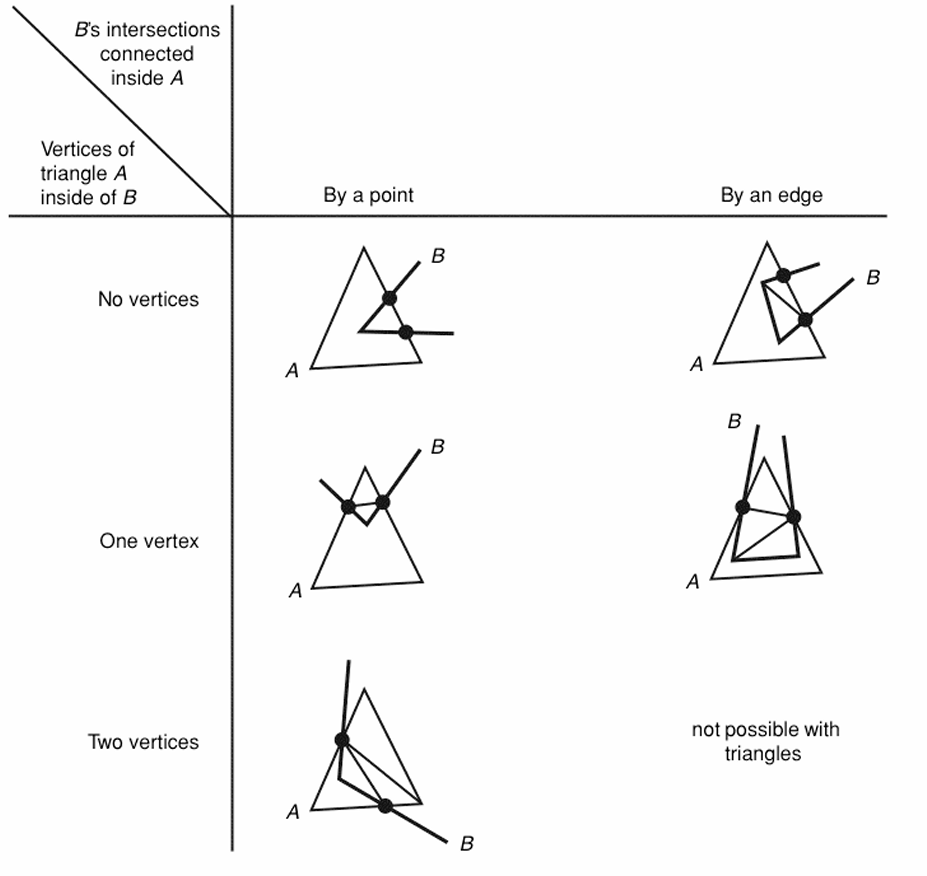
두 object를 겹쳤다고 생각하고, 두 오브젝트를 감싸는 sphere를 상상하여 각 mesh의 triangle을 sphere에 mapping한다. 그러면 source object와 target object의 triangle이 겹치는 경우가 존재한다
겹칠 수 있는 모든 가능한 Case는 위 표와 같다.
아이디어는, 겹친 정보를 토대로 두 object의 Mesh를 작은 삼각형 Mesh들로 쪼개는 것이다. 이후 Source Object와 Target Object의 서로 겹치는 삼각형은 어떤 점이 어떤 점과 Mapping되는지 쉽게 찾을 수 있다. 겹치지 않는 Vertex는, 가장 가까운 점을 찾아서 그 점과 mapping하면 모든 mapping이 가능해지고, mapping 관계를 찾으면 보간이 쉬워진다.
Image Morphing
두 이미지 간의 자연스러운 보간을 위한 기술. 만약 그냥 각 Pixel Color를 보간하게 되면 별로 자연스럽지 않다. Source image와 Target image의 특징을 분석하고, 두 이미지에 비슷한 특징이 존재한다면 그 특징을 자연스럽게 보간하면 자연스러운 Morphing이 가능하다. 과정은 다음과 같다.
- Find Correspondence (대응 관계)
- 원본 이미지와 대상 이미지 간의 대응되는 특징 점, Feature Point이나 특징적인 라인, Feature Line을 찾는다.
- 사용자가 특징 점이나 특징 선을 수동으로 정의할 수 있다.
- Intermediate Image (중간 이미지)
- 중간 단계 이미지를 생성한다.
- 두 이미지 간의 Feature Point, Line를 보간하여 딱 중간값 위치와 색깔을 만들어낸다.
- 원본 이미지 -> 중간 이미지 -> 최종 이미지로 보간한다.