고급컴퓨터그래픽스 3. Surfaces
건국대학교 고급컴퓨터그래픽스 김형석 교수님의 수업을 정리한 내용입니다.
Spline Curve를 사용하여 만들기
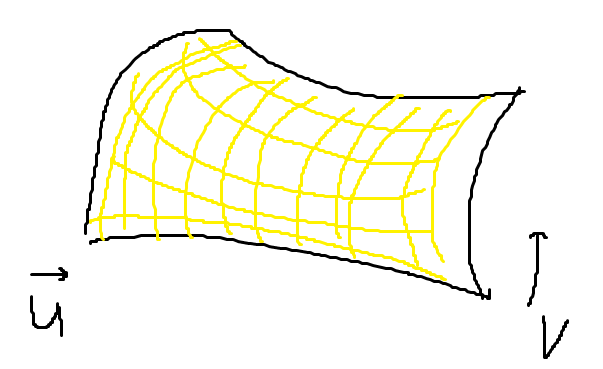
\[S: \vec{r}(u,v) = (x(u,v), y(u,v), z(u,v))\]곡면은 2개의 변수를 입력받는 벡터함수로 표현할 수 있다.^[Curved surface (곡면)]
[!tip] 이런 이미지를 상상{title}
선을 촘촘하게 모으는 것이 곡면이다. v 방향으로 곡선을 만들고, u 방향으로 그 곡선을 촘촘하게 모으면 그것이 바로 곡면이다.
계산이 쉽지만, 곡면 조절이 좀 힘들다. 캐드와 같이 정확도가 필요한 곳에서 이 방식을 사용한다.
Bezier Curve 사용
\[\vec{r}(u, v) = \sum_{j=0}^{m} \sum_{k=0}^{n} \vec{p}_{j,k} B_{j,m}(v) B_{k,n}(u)\]총 16개의 Control Point가 존재한다.
- 단점
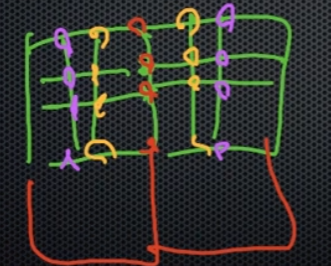
Bezier 패치로 곡면의 연속성을 만족시키려면
빨간점 위치가 붙어있어야 하고, 노란점이 대칭이어야 하고, 보라색 점이 대칭이어야 하는데
거기에 곡면이 추가로 더 붙으면 복잡해진다.
즉, 배지에 배치로는 C2 연속성을 만족시키기 매우 어렵다.
Subdivision 방법
Suybdivision도 여러 방법이 존재한다.
- Catmull78 방법 : 좋긴 한데 복잡하고 도형이 점점 많아진다
- Doo78 방법 : 계산이 너무 복잡하다
- …
현재는 Catmull78 방법을 보완한 것을 사용.
계산이 어렵다. 애니메이션같은 곳은 섭디비전 방법을 쓴다.
How?
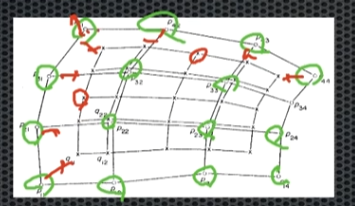
각 점의 안쪽 방향으로 점을 추가한다. 방향의 벡터는 면적의 안쪽 수직벡터를 구하는 방법으로 구할 수 있고, 얼마나 줄일건지는 재량껏 판단한다. Catmull 방법에선 평균치를 사용함.
따라서 Subdivision을 하면 크기가 작아질 수 밖에 없는데, 이를 해결하기 위해 크기를 먼저 키워놓고 Subdivision하는 방식을 쓰기도 함.
이걸 하면 전체적으로 다 부드러워지기 때문에, 이걸 원하지 않는다면 어떤 부분은 Subdivision의 영향을 받지 않게 하곘다 라고 표시를 해서 모양을 유지시킬 수 있음.
Bezier Patch (Surface)
곡면은 2개의 매개변수를 입력받아야 한다.
Cubic Bezier Patch:
\[P(u,v) = \sum_{i,j}^{3} B_{i}(u) P_{ij} B_{j}(v)\]Control Point를 \(P_{00}, P_{01}, \dots, P_{32}, P_{33}\) 총 16개를 입력받는다.
\(u = [0, 1]\), \(v = [0, 1]\) 범위를 갖고, Basis 함수인 \(B_{i}(u)\)는 Bezier Spline에서 사용한 Basis Function과 똑같다.
\[B_{0,3}(u) = (1-u)^3\] \[B_{1,3}(u) = 3u(1-u)^2\] \[B_{2,3}(u) = 3u^2(1-u)\] \[B_{3,3}(u) = u^3\]따라서, Control Point를 16개만 입력받으면 상대적인 위치 u, v를 \(P(u,v)\)에 넣으면 Bezier Patch로 보간된 곡면 위의 점 위치를 알 수 있다. (gl_Position).
[!tip] 테셀레이션으로 구현하려면?{title} TCS에서 Level을 정하고, Vertex를 16개씩 끊어 TES로 보낸다.
TES에선 quads로 받는다. 16개의 Vertex를
gl_in[0] ~ gl_in[15]를 사용하여 받는다.u = gl_TessCoord.x,v = gl_TessCoord.u임을 이용하여 각각 Basis 함수를 계산하고, 표현식을 사용해 점을 계산해서 최종적인gl_Position위치를 결정하면 된다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
/* TCS */
#version 400 core
layout(vertices = 16) out; // 4x4 Bezier Patch 제어점
// 테셀레이션 레벨 설정
uniform float tessLevelInner;
uniform float tessLevelOuter;
// TCS에서는 패치의 테셀레이션 레벨을 설정
void main() {
// 각 제어점을 TES로 전달
gl_out[gl_InvocationID].gl_Position = gl_in[gl_InvocationID].gl_Position;
// 테셀레이션 레벨 설정
if (gl_InvocationID == 0) {
gl_TessLevelInner[0] = tessLevelInner;
gl_TessLevelInner[1] = tessLevelInner;
gl_TessLevelOuter[0] = tessLevelOuter;
gl_TessLevelOuter[1] = tessLevelOuter;
gl_TessLevelOuter[2] = tessLevelOuter;
gl_TessLevelOuter[3] = tessLevelOuter;
}
}
/* TES */
#version 400 core
layout(quads, equal_spacing, cw) in;
// Bezier 기저 함수
float cubicBezierBasis(float t, int i) {
if (i == 0) return (1 - t) * (1 - t) * (1 - t);
else if (i == 1) return 3 * t * (1 - t) * (1 - t);
else if (i == 2) return 3 * t * t * (1 - t);
else if (i == 3) return t * t * t;
return 0.0;
}
void main() {
vec3 patchPoint = vec3(0.0);
// gl_TessCoord는 (u, v) 값을 나타냄 (곡면 위의 위치)
float u = gl_TessCoord.x;
float v = gl_TessCoord.y;
// Cubic Bezier Patch 보간 계산
for (int i = 0; i < 4; i++) {
for (int j = 0; j < 4; j++) {
float Bu = cubicBezierBasis(u, i);
float Bv = cubicBezierBasis(v, j);
patchPoint += Bu * Bv * gl_in[i * 4 + j].gl_Position.xyz;
}
}
gl_Position = vec4(patchPoint, 1.0); // 최종 패치 위의 점 위치
}