고급컴퓨터그래픽스 10. Ray Tracing
건국대학교 고급컴퓨터그래픽스 김형석 교수님의 수업을 정리한 내용입니다.
Ray Tracing
이론적으로는 광원에서 빛이 나오고, 빛이 여러군데에서 반사되어 최종적으로 나의 눈(카메라 렌즈)로 들어오는 것이다. 이 방법은 구현도 어렵고, 광원에서 무한한 양의 빛이 나오기 때문에 계산이 불가능하다.
따라서 실제 구현은 Ray-Casting 방식으로 구현된다. Ray-Casting은 반대로 내 눈에서 광선을 쏜다고 가정하고 빛을 계산하는 것이다.
- 내 눈의 위치에서 Ray를 쏜다.
- 쏜 Ray는 병렬적으로 계산된다. Ray와 Object의 교점을 구한다.
- Ray가 쏴진 위치를 \(x\), 교점의 위치를 \(x'\)라고 하자. 두 점의 위치를 Rendering Equation \(I(x,x')\)에 넣으면 \(x\)로 들어오는 빛의 세기와 색깔을 구할 수 있다.
- 빛의 양과 세기를 모두 더해서 최종적인 Color를 결정한다.
즉 실제 구현은, 화면의 Pixel마다 1000개~100만개 정도의 광원을 랜덤한 방향으로 쏜다. 각 광원이 다른 오브젝트와 만나는 교점을 계산해, 렌더링 방정식에 넣어서 나온 모든 빛의 양과 컬러를 조합한다. 이 방법으로 최종적으로 픽셀의 Color를 결정할 수 있다.
Render Equation
- \(\displaystyle I(x,x') = g(x,x')\left[ \epsilon(x,x') + \int_{S}\rho(x,x',x'')I(x',x'')dx'' \right]\)
- \(I(x,x')\) : \(x'\)에서 \(x\)로 전달되는 총 빛의 세기.
- \(g(x,x')\) : \(x\)와 \(x'\) 사이의 가시성을 고려한 함수.
- 만약 둘 사이에 가려진 물체가 있고
- 그 물체가 불투명하다면 \(g(x,x')=0\)이다.
- 그 물체가 반투명하다면, 투명 계수를 \(\alpha\)라고 하면 \(\displaystyle g(x,x')=\frac{1}{d^2}\alpha\)이다.
- 없다면, 빛의 세기가 거리에 따라 약해지는 효과를 고려하여 \(\displaystyle g(x,x')=\frac{1}{d^2}\)와 같다.
- 만약 둘 사이에 가려진 물체가 있고
- \(\epsilon(x,x')\) : \(x'\)에서 \(x\)로 직접 방출된 빛의 세기.
- 만약 교점에서 만난 빛이 광원이면 값이 존재한다.
- 광원이 아니면 \(\epsilon(x,x')=0\)이며, 반사광만 존재한다.
- \(\rho(x,x',x'')\) : \(x''\)에서 반사된 빛이 \(x'\)를 거쳐 \(x\)로 가는 반사 경로를 고려한 함수.
- \(I(x',x'')\) : \(x''\)에서 \(x'\)로 전달되는 총 빛의 세기.
- 따라서 \(\rho(x,x',x'')I(x',x'')\)는 \(x''\)에서 나온 빛이 \(x'\)를 통해 \(x\)로 들어오는 반사광을 의미한다.
렌더링 방정식을 전부 계산하는 것은 계산량이 너무 많으므로, 최대한 단순화 하는것이 중요하다.
- 재귀적인 계산이 끝도 없을 수 있다.
- 적분이 존재한다.
- 반사 함수 \(\rho(x,x',x'')\)가 무엇인가?
- 교점을 어떻게 구하고, 빨리 구할 수 있는가?
Recursion Solution
실험을 통해 재귀가 2~5 Step 정도만 되도 충분히 좋은 퀄리티의 결과를 낸다는 것을 알아낸다. 따라서 재귀의 Limit를 2~5 Step 정도로 걸어두고, 재귀 Level이 Limit 이상 넘어간다면 Background Color를 반환하도록 구현한다.
Integral Solution
그냥 Sum으로 근사한다. 게임에선 한 픽셀당 1000개 정도 Ray를 랜덤하게 뿌려 Sum하고, 영화같은 곳에선 픽셀당 100만개정도 Ray를 랜덤하게 뿌려 Sum한다.
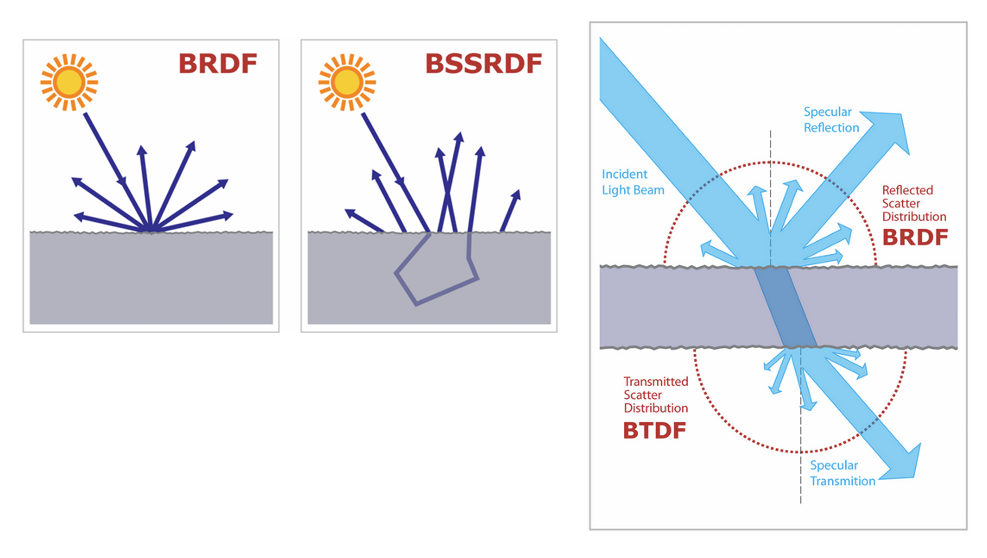
Surface Scattering
- BRDF : 표면에서 반사만을 다루는 함수. 많은 양은 정반사, 일부는 난반사하는 것을 고려한다.
- BSSRDF : 빛이 물체 내부로 들어가서 반사되는 것을 고려한 함수.
- BTDF : 빛의 물체를 통과하면서 굴절하는 것을 계산하는 함수.
- BSDF : BRDF + BSSRDF + BTDF를 모두 계산하는 함수.
BSDF
BSDF를 계산하는 다양한 모델이 존재한다.
- Phong Lighting Model
- Cook-Torrance Model
- Disney/Principled BSDF : 현재 게임 엔진에서 표준으로 사용한다고 함.
Phong Lighting Model
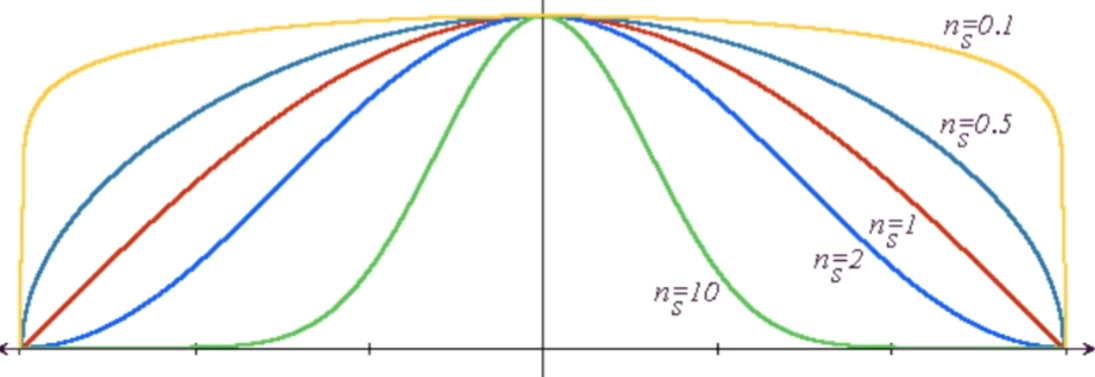
- \(\displaystyle \rho(x,x',x'') = k_{a}I +k_{s} I (\hat{r} \cdot \hat{v})^{n_{s}} + k_{d}I (\hat{n} \cdot \hat{l})\)
- Material Property
- \(k_{a}\) : 주변광 계수
- \(k_{d}\) : 난반사 계수
- \(k_{s}\) : 정반사 계수. 높을수록 Hightlight가 뚜렷해짐.
- \(n_{s}\) : 광택 계수. 정반사광의 퍼짐 정도를 결정함.
- Basic Color
물리적인 계산을 하지 않고, 그냥 관찰한 결과를 토대로 휴리스틱한 함수를 개발해 사용하는 반사 모델이다. 빛을 관찰해봤더니 대부분 다음과 같은 특징으로 근사할 수 있었다.
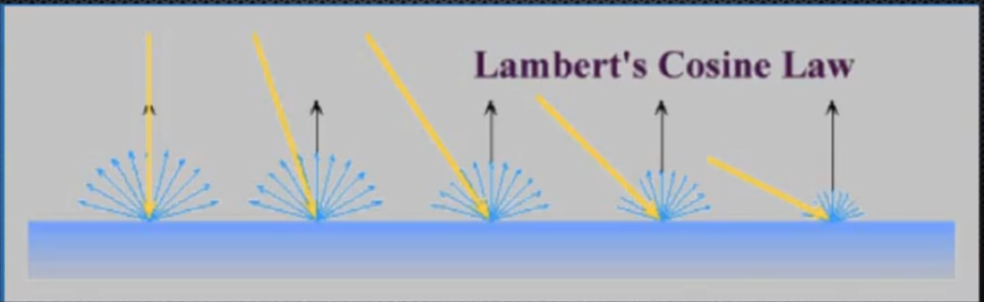
- Diffusion : 난반사되는 빛의 양은 모든 방향으로 균일하고, 수직에 가까울수록 난반사되는 빛의 양이 많고 수평에 가까울 수록 난반사되는 빛의 양이 적다. (Lambert’s Cosine Law)
- Specular : 정반사되는 빛의 양은 표면이 매끈할수록 많고, 거칠수록 적다.
- Ambient : 전체적으로 주변의 밝기를 균일하게 밝혀주는 주변광이 존재한다.
[!question]- How calculate to diffusion?{title}
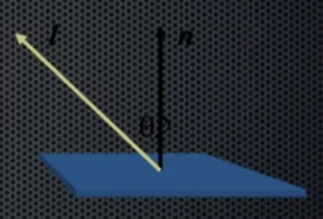
표면의 법선 벡터 \(\hat{n}\)과, 빛이 들어온 방향의 단위 벡터 \(\hat{l}\) 사이의 각을 \(\theta\)라고 하자. 난반사되는 빛의 양은 \(\cos \theta\)에 비례하다. \(\cos \theta\)는 두 벡터를 내적한 것과 같다. \(\displaystyle \cos \theta = \hat{n} \cdot \hat{l}\)
면의 색깔 계수를 \(k_{d}\), 들어온 빛의 세기를 \(I\)라고 하면 \(I_{d} = k_{d}I\cos \theta = k_{d}I (\hat{n} \cdot \hat{l})\)로 계산 가능하다.
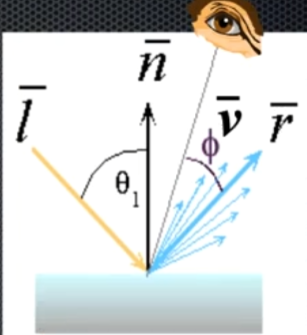
[!question]- How calculate to specular?{title}
\(\hat{r}\)를 정반사 되는 벡터 방향, \(\hat{v}\)를 관측 방향일 때 \(\hat{r} \cdot \hat{v} = \cos \phi\)로 \(\phi\)를 정의하자. \(n_{s}\)는 표면의 매끈한 정도를 나타내는 계수다. \(\phi\to0\)일 수록 정반사되는 빛이 많이 관측되고, 따라서 빛의 양이 가장 밝아야 한다. \(I_{s}\)는 \(\cos \phi\)와 비례하다. 표면이 매끈할수록 정반사가 일어나고, 그렇지 않을수록 난반사가 일어난다. 이를 고려하여 \((\cos \phi)^{n_{s}}\)를 사용한다. 최종적으로 정반사되는 빛의 양은 \(\displaystyle I_{s} = k_{s} I (\cos \phi)^{n_{s}}\)로 계산한다.
[!question]- How calculate to ambient?{title}
단순히 주변광 세기만 고려하면 된다. \(I_{a} = k_{a}I\)
Disney BSDF
Disney BSDF에서 사용하는 Material의 Property는 다음과 같다.
- Base Color
- Metallic : 표면이 금속인가? 금속은 반사율이 높고, 색깔이 반사광에 크게 의존된다.
- Roughness : 표면의 거칠기의 정도. 거칠수록 반사광이 세지고 매끄러울수록 정반사가 많아진다.
- Specular : 비금속 표면의 반사 강도.
- Clearcoat : 얇은 반사층? 섬세한 광택을 표현.
- Sheen : 섬유나 천과 같은 재질의 반사 효과 고려
- Subsurface : 빛이 표면 아래로 들어가서 퍼지는 산란 효과.
- Transmission : 투과율
Faster Intersection
Ray Tracing을 위해선 주변의 모든 Mesh 구조를 다 알고 있어야 한다. 최적화 아이디어를 살펴보자.
- 복잡한 Polygon Mesh와 빛이 충돌했는지 일일히 검사하는건 시간이 오래 걸린다. 따라서 Polygon Mesh를 감싸는 단순한 모양의 Bounding Volume과 충돌 체크를 한다.
- 그 중 만나는 것만 따로 Polygon 충돌 체크를 하면, 충돌할 가능성이 없는 오브젝트를 빠르게 걸러줄 수 있다.
Bounding Volume
물체를 감싸는 단순한 모양. Ray와 교점 검사를 빠르게 하기 위해 사용한다.
- Bounding Sphere
- Axix-Aligned Bounding Box (AABB)
- Oriented Bounding Box (OBB)
Bounding Volume Hierarchies (BVH)
Bounding Volume Hierarchies (BVH) : BS, ABB, OBB의 장점만 취한 것
Spartial Partitioning
- Uniform Grid
- Octree
- K-d Tree
균일하게 배치되있는건 BVH가 딱히 극적인 효과가 안나올 수 있음. 그런경우는 Uniform Grid가 더 효율적일 수 이쏙 ,보통 일반 공간은 부분 공간 하나에 삼각형 100개정도가 들어가도록 grid를 나눔.
쪼개는 방법은 Octree를 사용해서 효율적으로 한 사각형 안에 프리미티브 100개정도 들어가도록 자를 수 있는다. 삼각형이 100만개가 넘어가면 Octree를 쓰는게 효율적이고 1000개정도밖에 없다면 오히려 오버헤드가 발생할 수 있다.
실제로 알고리즘을 쓰기 위해선 \(O(n)\)의 상수를 봐야한다. \(O(n^2)\)이라도 앞의 상수가 0.0001이라면 어느정도 n까진 충분히 쓸 수 있다. \(O(n)\)이라도 앞의 상수가 100만이라면, n이 100만이 넘기 전까지는 오히러 \(n^2\)짜리가 더 효율적일 수 있다는 것.
실제로 게임에서는 AABB, Boundry Sphere가 가장 많이 쓰인다. 캐드와 같은 곳에선 kd-tree를 많이 쓴다. (얼마나 빨리 계산해야 하냐 vs 얼마나 정확하게 계산해야 하냐)
Testing : Canal Box
[!NOTE]- Canal Box Test{title}
기본 상태의 Canal Box.
Diffuse Reflection만 적용한 모습. 빛이 반사만 되고 흡수를 구려하지 않으면 물체가 플라스틱처럼 보인다.
다른 물체의 존재를 고려하면 Hard Shadow가 생긴다.
Point Light -> Area Light
Indirect Illumination 추가.
Glossy(광택) Materials 고려.