고급컴퓨터그래픽스 1. Curves

건국대학교 고급컴퓨터그래픽스 김형석 교수님의 수업을 정리한 내용입니다.

Circle

[!note]- 원 그리기{title} \((x_{c}, y_{c})\)가 중심이고, 반지름이 \(r\)인 원의 방정식은 다음과 같다.

\[y=y_{c} \pm \sqrt{ r^2 - (x-x_{c})^2 }\] \[f(x,y) = (x-x_{c})^2+(y-y_{c})^2-r^2=0\] \[x(\theta) = x_{c}+ r\cos \theta, ~~~y(\theta)= y_{c} + r\sin \theta\]

첫번째 방식이 Explicit, 두번째 방식이 Implicit, 세번째 방식이 Parametric.^[Equation (방정식)#방정식의 모양]

Explicit Equation 사용

\[y=y_{c} \pm \sqrt{ r^2 - (x-x_{c})^2 }\]

x를 \(x_{c}-r \leq x \leq x_{c}+r\) 범위에서 for문 돌려서 dx (=0.1, 0.05)만큼 증가시키면 그릴 수 있을 듯.

하지만 단점이 있다.

1. Sqrt 연산은 계산이 느리다.

한두개면 괜찮은데, 방대한 반복 연산을 해야하기 때문에 Sqrt같은 복잡한 연산은 피하는게 좋다.

1. 간격이 Uniform하지 않다.

x가 0.1씩 증가하면, 어떨땐 y가 조금 감소하지만 어떨땐 y가 크게 감소해서 빈 공간이 생길 수 있다. => 빈칸 사이에 선을 그려서 채우는 방법을 쓸 수 있지만, 부자연스러움.

Parametric Equation 사용

\[x(\theta) = x_{c}+ r\cos \theta, ~~~y(\theta)= y_{c} + r\sin \theta\]

Polar coordinate (극좌표계) 를 사용한다.

이걸 사용하면, \(\theta\)를 0.1씩 증가시키면 원 호가 균일하게 그려져서, Explicit Equation을 사용했을 때 단점을 해결할 수 있다.

하지만, sin, cos가 있어서 아직 계산이 복잡하다.

또, 각도를 몇도씩 증가시키는게 좋을지 원의 크기에 따라 달라진다.

• 원이 너무 작으면, 1도씩 증가하면 중복 픽셀이 생기고,
• 원이 너무 크면, 1도씩 증가하면 픽셀이 듬성듬성 채워질 것이다.

Implicit Equation 사용

\[f(x,y) = (x-x_{c})^2+(y-y_{c})^2-r^2=0\]

이걸 도대체 어떻게 쓰는데?

이 방정식에는 중요한 의미가 있다.

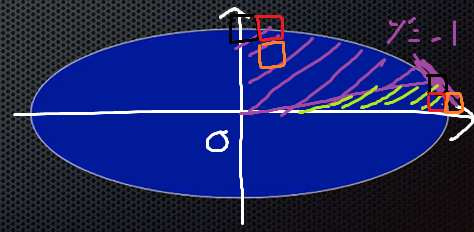
\((x, y)\) 값을 \(f(x, y)\)에 넣었을 때 0이 나오면 원의 테두리, +면 원의 밖, -면 원의 안쪽에 있다는 의미다.

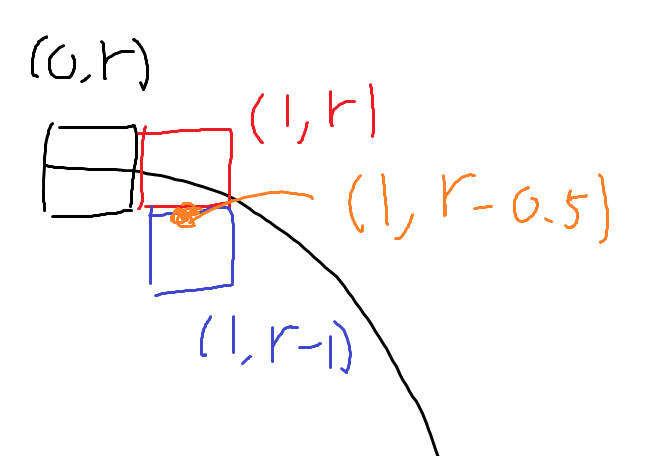
픽셀 한칸 단위를 1이라고 하면, \((x, y)\) 점에서 시작하여 \(x+1\)일 때 픽셀을 어디에 그릴지 \(f(x, y)\)에 \((x+1, y-0.5)\) 또는 \((x+1, y+0.5)\)를 넣어 나온 결과로 판단하는 방법이다.

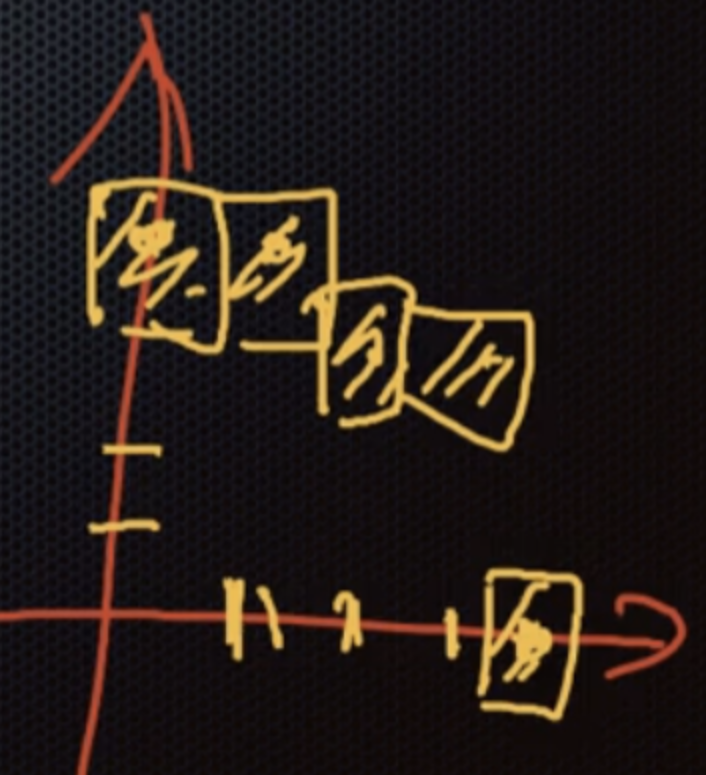
예를들어, \((0, r)\)에서 시작한다.

\(f(x, y)\)에 그려질 가능성이 있는 두 픽셀의 중간점인 \((x+1, y-0.5)\)를 넣는다. \(p_{k} = f(x_{k}+1, y_{k}-0.5)\)라고 정의했을 때, \(p_{0} < 0\)이면 파란색 점을 그리고, \(p_{0} \geq 0\)이면 빨간색 점을 그리면 된다.

즉, 현재 그리는 점의 좌표를 \((x_{k}, y_{k})\)라고 하면 다음 그릴 점의 좌표는 \((x_{k+1}, y_{k+1})\)이다.

위 곡선의 경우 \(p_{k}\)와 \(y_{k+1}\)는 다음과 같다.

\[p_{k} = f(x_{k}, y_{k}-0.5)\] \[y_{k+1} = \begin{cases} y_{k}~~~~~~~~~~~~ if~~p_{k} < 0 \\ y_{k}-1 ~~~~~if~~p_{k} \geq 0\end{cases}\]

위 두 값은 곡선의 기울기에 따라 알맞게 설정하면 된다. 이 방법을 Midpoint Circle Drawing 라고 부른다.

위 방법을 사용하면 이런 장점이 있다.

• 덧셈, 곱셈만 있어 계산이 간단하다
• 픽셀이 한칸씩 움직여 간격이 Uniform해진다.

좀 더 계산량을 줄일 수 없을까?

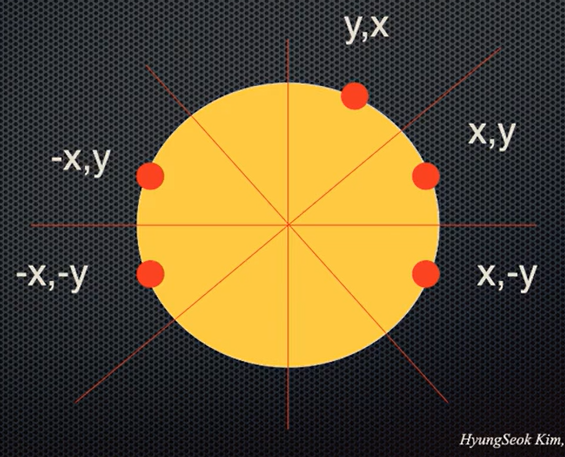
1. Symmetry(대칭성)을 이용한다.

원의 1/8만 그려도 나머지는 대칭성을 이용해서 점을 찍을 수 있다.

즉, 한번 계산할 때마다 8개의 점을 찍으면 됨.

1. 원의 좌표를 계산할 때, 원점을 기준으로 계산하여 나온 결과에 \((x_{c}, y_{c})\)를 더해 이동시킨다.

이렇게 하면 \(f(x, y) = x^2 + y^2 - r^2\)로 간단히 쓸 수 있고, 나온 결과에 +\(x_{c}\), +\(y_{c}\)를 해주면 된다.

1. 이전의 계산한 \(p_{k}\)를 바탕으로 \(p_{k+1}\)을 계산한다.

\[p_{k+1} - p_{k} = (x_{k+1}+1)^2 + (y_{k++1}-0.5)^2 - r^2 - (x_{k}+1)^2 - (y_{k}-0.5)^2 + r^2\]

\(x_{k+1} = x_{k}+1\)이므로

\[= (x_{k}+2)^2 + (y_{k+1}-0.5)^2 - (x_{k}+1)^2 - (y_{k}-0.5)^2\]

\(p_{k} < 0\)인 경우, \(y_{k+1} = y_{k}\)

\[=2x_{k}+3 = 2x_{k+1}+1\]

\(p_{k} \geq 0\)인 경우, \(y_{k+1}=y_{k}-1\)

\[= 2x_{k}+3 + (y_{k} - 1.5)^2 - (y_{k}-0.5)^2\] \[=2x_{k}+3+y_{k}^2-3y_{k}+2.25-y_{k}^2+y_{k}-0.25\] \[=2x_{k}-2y_{k}+5 = 2x_{k+1}-2y_{k+1}+1\]

OK, \(p_{0}\)만 알면 위 정보를 토대로 \(p_{1}, p_{2}, \dots\)를 간단하게 알 수 있겠다.

\[p_0 = f(1, r-0.5)\] \[= 1 + (r-0.5)^2 - r^2\] \[= 1.25 - r\]

구현 의사코드

\((0, r)\)에서 시작하여 1/8만큼만 그리면 된다. => x의 값이 y의 값보다 커질 때까지 Loop 돌면 됨.

void drawCircle(Point middle, float radius)
{
    int x = 0, y = radius;
    float p_k = 1.25 - radius // 처음에 p_0에서 시작

    while (x <= y)
    {
        current.x += 1; // current.x = x_{k+1}가 됨
        if (p_k < 0)
        {
            // p_{k+1} - p_k = 2x_{k+1} + 1
            p_k += (2 * x) + 1
        }
        else
        {
            y -= 1;
            // p_{k+1} - p_k = 2x_{k+1}-2y_{k+1}+1
            p_k += (2 * x) - (2 * y) + 1; 
        }
        
        x += middle.x; y += middle.y;
        plot(x, y); plot(-x, y); plot(x, -y); plot(-x, -y);
        plot(y, x); plot(-y, x); plot(y, -x); plot(-y, -x);
        x -= middle.x; y -= middle.y;
    }
}

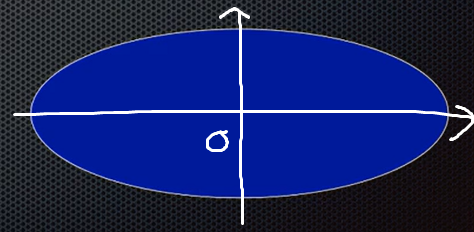
[!NOTE]- 타원 그리기{title}

타원은 두 조첨의 좌표와, 두 초점 사이의 거리의 합(d)를 알아야 한다.

\[\sqrt{ (x-x_{1})^2 + (y-y_{1})^2 } + \sqrt{ (x-x_{2})^2 + (y-y_{2})^2 } = d\]

타원의 방정식은 위와 같은데, 너무 더럽다.

정직하게 장축, 단축이 x축, y축 위에 있고 원점이 중심이면 훨씬 간결하게 만들 수 있다.

\[\left( \frac{x}{r_{x}} \right)^2+\left( \frac{y}{r_{y}} \right)^2=1\]

\(r_{x}\) = 장축의 길이, \(r_{y}\) = 단축의 길이

이걸 그리고, 타원을 회전해서 \((x_{c}, y_{c})\)만큼 움직이면 임의의 타원을 그리는 것과 같음.

이제 \(f(x, y)\) 설정하고, \(p_{k}\)와 \(y_{k+1}\)을 정해서 \(p_{k+1} - p_{k}\)를 구하면 된다.

\[f(x,y) = \left( \frac{x}{r_{x}} \right)^2+\left( \frac{y}{r_{y}} \right)^2 -1 = 0\]

타원은 1/4만큼만 그리면 된다. \((0, r_{y})\) ~ \((r_{x}, 0)\) 범위를 그리면 됨.

주의할 점이, 기울기 \(-1\)을 기준으로 \(p_{k}\), \(x_{k+1}\), \(y_{k+1}\)이 바뀌어야 한다.

보라색 범위에선 x가 1 증가할 때 y가 증가하지 않거나 -1 만큼 감소할 것이고, 연두색 범위에선 y가 1 감소할 때 x가 증가하지 않거나 +1 만큼 증가할 것이다.

\[p_{k} = \begin{cases} f(x_{k}+1, y_{k}-0.5)~~~~~ if~~ \frac{dy}{dx} < -1 \\ f(x_{k}+0.5, y_{k}-1) ~~~~~if~~ \frac{dy}{dx} \geq -1 \end{cases}\]

• 보라색 범위

\[x_{k+1} = x_{k} + 1\] \[y_{k+1} = \begin{cases} y ~~~~~~~~~~if~~ p_{k} < 0 \\ y-1 ~~~if~~ p_{k} \geq 0 \end{cases}\]

• 연두색 범위

\[x_{k+1} = \begin{cases} x ~~~~~~~~~~if~~ p_{k} < 0 \\ x+1 ~~~if~~ p_{k} \geq 0 \end{cases}\] \[y_{k+1} = y_{k} - 1\]

1) \(\frac{dy}{dx} < -1\)일 때, \(p_{k+1} - p_{k}\)

\[p_{k+1} - p_{k} = \left( \frac{x_{k+1}+1}{r_{x}} \right)^2 + \left( \frac{y_{k+1}-0.5}{r_{y}} \right)^2 - 1 - \left( \frac{x_{k}+1}{r_{x}} \right)^2 - \left( \frac{y_{k}-0.5}{r_{y}} \right)^2 + 1\] \[= \left( \frac{x_{k}+2}{r_{x}} \right)^2 + \left( \frac{y_{k+1}-0.5}{r_{y}} \right)^2 - \left( \frac{x_{k}+1}{r_{x}} \right)^2 - \left( \frac{y_{k}-0.5}{r_{y}} \right)^2\] \[= \frac{2x_{k}+3}{{r_{x}}^2} + \left( \frac{y_{k+1}-0.5}{r_{y}} \right)^2 - \left( \frac{y_{k}-0.5}{r_{y}} \right)^2\]

if \(p_{k} < 0\) => \(y_{k+1} = y\)

\[p_{k+1} - p_{k} = \frac{2x_{k}+3}{{r_{x}}^2} = \frac{2x_{k+1}+1}{{r_{x}}^2}\]

if \(p_{k} \geq 0\) => \(y_{k+1} = y_{k}-1\)

\[p_{k+1} - p_{k} = \frac{2x_{k}+3}{{r_{x}}^2} + \left( \frac{y_{k}-1.5}{r_{y}} \right)^2 - \left( \frac{y_{k}-0.5}{r_{y}} \right)^2\] \[= \frac{2x_{k}+3}{{r_{x}}^2} + \frac{-2 y_{k} + 2}{{r_{y}}^2}\] \[= \frac{2x_{k+1}+1}{{r_{x}}^2} + \frac{-2y_{k+1}}{{r_{y}}^2}\]

2) \(\frac{dy}{dx} \geq -1\)일 때, \(p_{k+1} - p_{k}\)

\[p_{k+1}-p_{k} = \left( \frac{x_{k+1}+0.5}{r_{x}} \right)^2 + \left( \frac{y_{k+1}-1}{r_{y}} \right)^2 -1 - \left( \frac{x_{k}+0.5}{r_{x}} \right)^2 - \left( \frac{y_{k} -1}{r_{y}} \right)^2 +1\] \[= \left( \frac{x_{k+1}+0.5}{r_{x}} \right)^2 - \left( \frac{x_{k}+0.5}{r_{x}} \right)^2 + \left( \frac{y_{k}-2}{r_{y}} \right)^2 - \left( \frac{y_{k}-1}{r_{y}} \right)^2\] \[= \left( \frac{x_{k+1}+0.5}{r_{x}} \right)^2 - \left( \frac{x_{k}+0.5}{r_{x}} \right)^2 + \frac{-2y_{k} + 3}{{r_{y}}^2}\]

if \(p_{k} < 0\) => \(x_{k+1} = x\)

\[p_{k+1} - p_{k} = \frac{-2y_{k} + 3}{{r_{y}}^2} = \frac{-2y_{k+1} + 1}{{r_{y}}^2}\]

if \(p_{k} \geq 0\) => \(x_{k+1} = x+1\)

\[p_{k+1} - p_{k} = \left( \frac{x_{k}+1.5}{r_{x}} \right)^2 - \left( \frac{x_{k}+0.5}{r_{x}} \right)^2 + \frac{-2y_{k} + 3}{{r_{y}}^2}\] \[= \frac{2x_{k} + 2}{{r_{x}}^2} + \frac{-2y_{k} + 3}{{r_{y}}^2}\] \[= \frac{2x_{k+1}}{{r_{x}}^2} + \frac{-2y_{k+1} + 1}{{r_{y}}^2}\]

3) \(p_{0}\)

\[p_{0} = f(x_{0} + 1, y_{0} - 0.5)\] \[= f(1, r_{y} - 0.5)\] \[= \left( \frac{1}{r_{x}} \right)^2 + \left( \frac{r_{y}-0.5}{r_{y}} \right)^2 - 1\] \[= \frac{1}{{r_{x}}^2} + \left( 1- \frac{0.5}{r_{y}} \right)^2 - 1\]

구현 의사코드

\((0, r)\)에서 시작하여 1/4만큼만 그리면 된다. => y의 값이 0과 같거나 작아질 때까지 Loop 돌면 됨.

회전 => (x, y) 벡터에 Rotate Matrix (회전 행렬) 적용.

// radius.x = x axis radius, radius.y = y axis axis
void drawEllipse(Point middle, Point radius, float rotateRadian)
{
    Vector current = new Vector(0, radius.y);
    Vector squareRadius = new Vector(square(radius.x), square(radius.y));
    Matrix rotate = getRotateMatrix(rotateRadian);
    float p_k = 1 / square(radius.x) + square(1 - 0.5/radius.y) - 1; // 처음에 p_0에서 시작

    while (current.y > 0)
    {
        float dy_dx = // 타원의 방정식을 Explicit으로 표현 후 미분하여 값을 넣는 식으로 계산;

        if (dy_dx < -1)
        {
            current.x += 1; // current.x = x_{k+1}가 됨
            
            if (p_k < 0)
            {
                // p_{k+1} - p_k = (2x_{k+1} + 1) / (r_x)^2
                p_k += ((2*current.x) + 1) / squareRadius.x
            }
            else
            {
                current.y -= 1;
                // p_{k+1} - p_k = (2x_{k+1} + 1) / (r_x)^2 - 2y_{k+1}/(r_y)^2
                p_k += ((2*current.x) + 1) / squareRadius.x - (2*current.y) / squareRadius.y; 
            }
        }
        else
        {
            current.y -= 1; // current.y = y_{k+1}가 됨
            
            if (p_k < 0)
            {
                // p_{k+1} - p_k = (-2y_{k+1} + 1) / (r_y)^2
                p_k += ((2*current.y) + 1) / squareRadius.y
            }
            else
            {
                current.x += 1;
                // p_{k+1} - p_k = (2x_{k+1}) / (r_x)^2 + (-2y_{k+1} + 1)/(r_y)^2
                p_k += (2*current.x) / squareRadius.x + (-2*current.y + 1) / squareRadius.y; 
            }
        }

        Vector temp = current;
        current = rotate * current;
        current += middle;
        plot(current.x, current.y);
        plot(-current.x, current.y);
        plot(current.x, -current.y);
        plot(-current.x, -current.y);
        current = temp;
    }
}

to GPT

void drawEllipse(Point middle, Point radius, float rotateRadian)
{
    float rx = radius.x;
    float ry = radius.y;
    float rx2 = rx * rx;
    float ry2 = ry * ry;
    float twoRx2 = 2 * rx2;
    float twoRy2 = 2 * ry2;

    float x = 0;
    float y = ry;

    // 초기 결정 변수
    float p1 = ry2 - (rx2 * ry) + (0.25f * rx2);

    float dx = twoRy2 * x;
    float dy = twoRx2 * y;

    Matrix rotate = getRotateMatrix(rotateRadian);

    // 영역 1
    while (dx < dy)
    {
        // 회전 및 이동
        Vector current(x, y);
        Vector rotatedCurrent = rotate * current;
        rotatedCurrent += middle;

        // 점 그리기
        plot(rotatedCurrent.x, rotatedCurrent.y);
        plot(rotatedCurrent.x, 2 * middle.y - rotatedCurrent.y);
        plot(2 * middle.x - rotatedCurrent.x, rotatedCurrent.y);
        plot(2 * middle.x - rotatedCurrent.x, 2 * middle.y - rotatedCurrent.y);

        if (p1 < 0)
        {
            x++;
            dx += twoRy2;
            p1 += dx + ry2;
        }
        else
        {
            x++;
            y--;
            dx += twoRy2;
            dy -= twoRx2;
            p1 += dx - dy + ry2;
        }
    }

    // 영역 2
    float p2 = (ry2) * pow(x + 0.5f, 2) + (rx2) * pow(y - 1, 2) - (rx2 * ry2);

    while (y >= 0)
    {
        // 회전 및 이동
        Vector current(x, y);
        Vector rotatedCurrent = rotate * current;
        rotatedCurrent += middle;

        // 점 그리기
        plot(rotatedCurrent.x, rotatedCurrent.y);
        plot(rotatedCurrent.x, 2 * middle.y - rotatedCurrent.y);
        plot(2 * middle.x - rotatedCurrent.x, rotatedCurrent.y);
        plot(2 * middle.x - rotatedCurrent.x, 2 * middle.y - rotatedCurrent.y);

        if (p2 > 0)
        {
            y--;
            dy -= twoRx2;
            p2 += rx2 - dy;
        }
        else
        {
            x++;
            y--;
            dx += twoRy2;
            dy -= twoRx2;
            p2 += dx - dy + rx2;
        }
    }
}

Curves

여러개의 점을 Fitting하는 적당한 곡선을 찾는 방법. 점을 반드시 지나가게 하는 방법을 보간(Interpolation)한다고 한다.

Polynomial Curve을 사용한다. 다항 곡선은 \(\displaystyle P(u) = \sum_{k=0}^{n} P_{k}B_{k}(u) = UMP\)와 같은 표현식을 갖는다. \(B_{k}\)는 Basic Function이며 어떤 Basic Function을 사용하냐에 따라서 Curve의 종류가 다르다.

Bezier Curve

• Bezier Curve : \(\displaystyle P(u) = \sum_{k=0}^{n} P_{k} B_{k,n}(u)\)
  • \(P_{k}\) = Control Point의 Position.
  • \(B_{k, n}(u) = nCk \cdot u^k (1-u)^{n-k}\)
• Cubic Bezier Curve : \(\displaystyle P(u) = \sum_{k=0}^{3} P_{k} B_{k,3}(u) =\left[ \begin{matrix} u^3 & u^2 & u & 1 \end{matrix} \right] \left[ \begin{matrix} 1 & 3 & -3 & 1 \\ 3 & -6 & 3 & 0 \\ -3 & 3 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{matrix} \right] \left[ \begin{matrix} p_{i} \\ p_{i+1} \\ p_{i+2} \\ p_{i+3} \end{matrix} \right]\)
  • \(B_{0,3}(u) = (1-u)^3\)
  • \(B_{1,3}(u) = 3u(1-u)^2\)
  • \(B_{2,3}(u) = 3u^2(1-u)\)
  • \(B_{3,3}(u) = u^3\)

점 n개를 사용해서 양 끝점을 반드시 지나고, 중간 점을 가까이 지나가게 하는 곡선을 생성한다. 파라미터 \(u\)는 \(u \in [0, 1]\) 범위를 갖는다. 차수가 높을 수록 Basis Function 계산이 힘들어지기 때문에, 일반적으로 Cubic(3차) Bezier Curve를 사용한다.

Cubic Bezier Curve는 컨트롤 포인트 4개 사이의 곡선을 보간한다. \(p_{i+1}, p_{i+2}\)가 지나는 것을 보장하지 않는다.

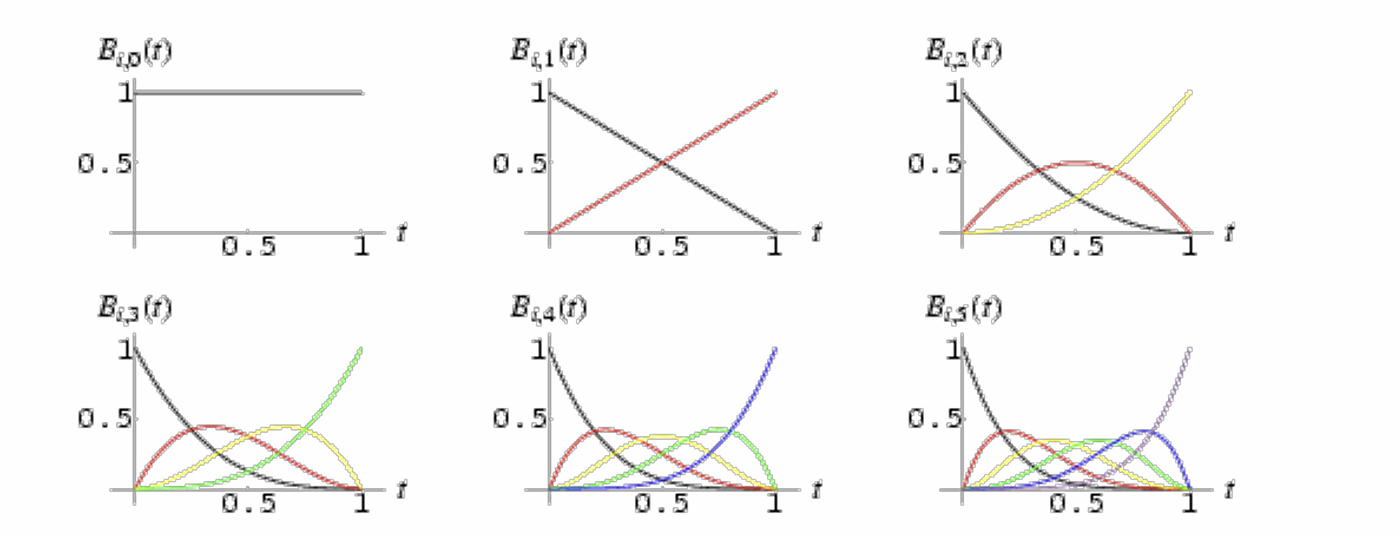
[!tip]- Info Basis Function{title} Basis Function을 Convex Combination(컨벡스 콤비네이션) 방식으로 조합된다. Convex Combination이란, Basis Function는 전부 0 이상이며, 전부 더하면 1이 나오도록 설계되었다는 뜻이다.

• 1차 Basis Function
  • \(B_{0,1}(u) = 1-u\)
  • \(B_{1,1}(u) = u\)
• 2차 Basis Function
  • \(B_{0,2}(u) = (1-u)^2\)
  • \(B_{1,2}(u) = 2u(1-u)\)
  • \(B_{2,2}(u) = u^2\)
• 3차 Basis Function
  • \(B_{0,3}(u) = (1-u)^3\)
  • \(B_{1,3}(u) = 3u(1-u)^2\)
  • \(B_{2,3}(u) = 3u^2(1-u)\)
  • \(B_{3,3}(u) = u^3\)
• n차 Basis Function
  • \(B_{k, n} = nCk \cdot u^k (1-u)^{n-k}\)

Hermite Curve

• \(\displaystyle P(u) = \sum_{k=0}^{3} g_{k} H_{k}(u) P(u) = \left[ \begin{matrix} u^3 & u^2 & u & 1 \end{matrix} \right] \left[ \begin{matrix} 2 & -2 & 1 & 1 \\ -3 & 3 & -2 & -1 \\ 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 \end{matrix} \right] \left[ \begin{matrix} p_{i} \\ p_{i+1} \\ p_{i}' \\ p_{i+1}' \end{matrix} \right]\)
  • \(g_{0} = p_{0}\), \(g_{1} = p_{1}\), \(g_{2} = p_{0}'\), \(g_{3} = p_{1}'\)
  • \(H_{0}(u) = 2u^3 - 3u^2 + 1\)
  • \(H_{1}(u) = -2u^3 + 3u^2\)
  • \(H_{2}(u) = u^3 -2u^3 + u\)
  • \(H_{4}(u) = -2u^3 - u^2\)

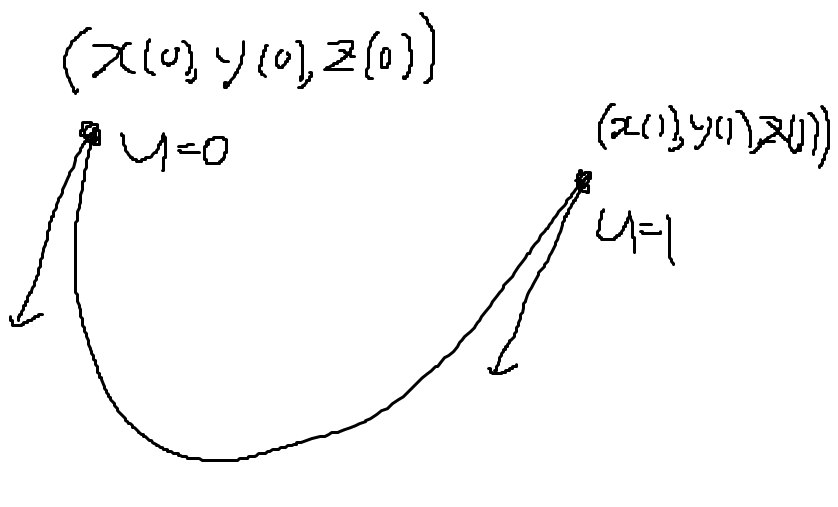
두 점과, 두 점에서의 기울기를 통해 두 점을 지나가는 곡선을 생성한다. 파라미터 \(u\)는 \(u \in [0, 1]\) 범위를 갖는다. \(g_{k}\)의 \(p_{0}\), \(p_{1}\)를 시작점과 끝점, \(p_{0}'\), \(p_{1}'\) 를 시작점과 끝점에서의 기울기라고 정의한다.

\(H_{k}(u)\)는 Basis Function라고 불리며, 위와 같다.

[!tip]- Basic Function의 유도 과정{title}

각 성분마다 4개의 미지수가 존재한다. 시작점과 끝점 좌표, 시작점에서의 기울기와 끝점에서의 기울기를 정해주면 4개의 방정식이 주어지므로 곡선 하나를 특정할 수 있게 된다. 시작점의 u를 0, 끝점의 u를 1이라고 하자.

\[x'(u) = 3a_{x}u^2 + 2b_{x}u + c_{x}\] \[x(0) = d_{x}, ~~ x(1) = a_{x} + b_{x} + c_{x} + d_{x}\] \[x'(0) = c_{x}, ~~x'(1) = 3a_{x} + 2b_{x}\]

이걸 가지고 \(a_{x}, b_{x}, c_{x}, d_{x}\)를 구하면

\[a_{x} = 2x(0) - 2x(1) + x'(0) - 2x'(1)\] \[b_{x} = -3x(0) + 3x(1) - 2x'(0) - x'(1)\]

\(c_{x}=x'(0)\), \(d_{x} = x(0)\)

이 정보를 가지고 \(x(u)\)를 다르게 표현해보자.

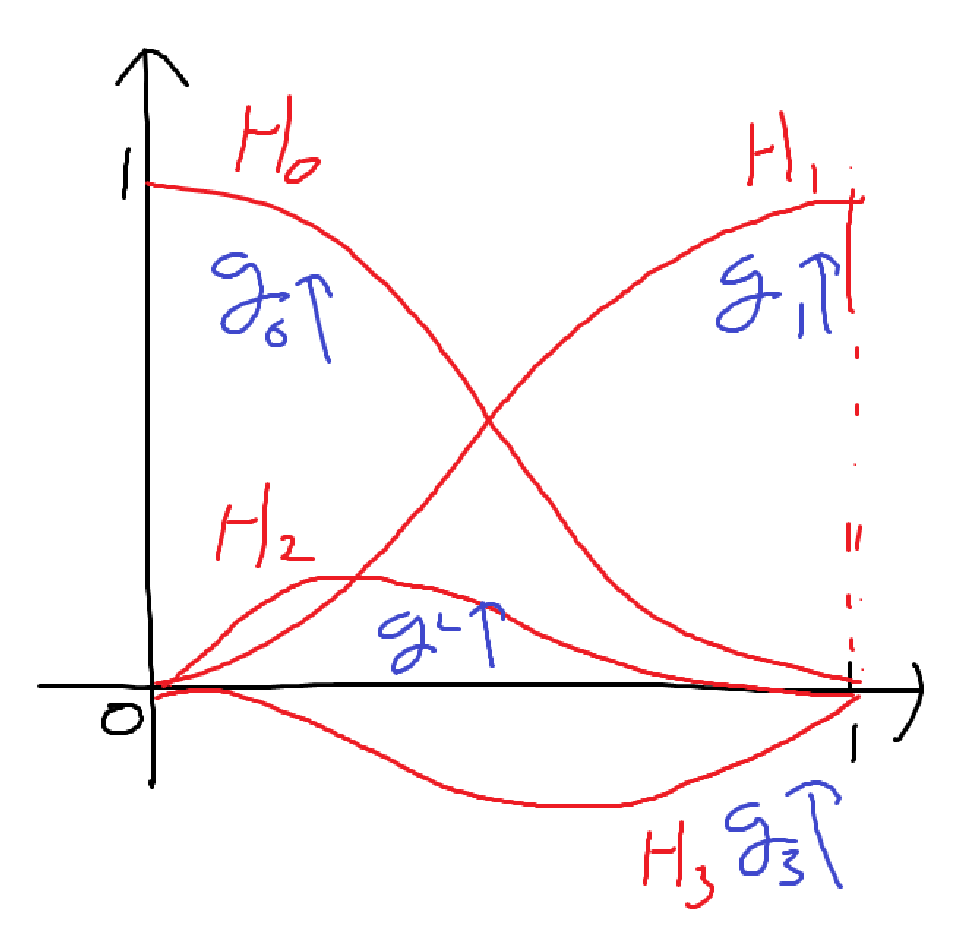
\[x(u) = a_{x}u^3 + b_{x}u^2 + c_{x}u + d_{x}\] \[= \begin{bmatrix} u^3 & u^2 & u & 1\\ \end{bmatrix} \cdot \begin{bmatrix} a_{x}\\ b_{x} \\ c_{x} \\ d_{x} \end{bmatrix}\] \[= \begin{bmatrix} u^3 & u^2 & u & 1\\ \end{bmatrix} \cdot \begin{bmatrix} 2x(0) - 2x(1) + x'(0) - 2x'(1)\\ -3x(0) + 3x(1) - 2x'(0) - x'(1) \\ x'(0) \\ x(0) \end{bmatrix}\] \[= \begin{bmatrix} u^3 & u^2 & u & 1\\ \end{bmatrix} \begin{bmatrix} 2 & -2 & 1 & -2\\ -3 & 3 & -2 & -1 \\ 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} x(0) \\ x(1) \\ x'(0) \\ x'(1) \end{bmatrix}\] \[= \begin{bmatrix} 2u^3 - 3u^2 + 1 & -2u^3 + 3u^2 & u^3 - 2u^2 + u & -2u^3 - u^2\\ \end{bmatrix} \begin{bmatrix} x(0) \\ x(1) \\ x'(0) \\ x'(1) \end{bmatrix}\] \[= \begin{bmatrix} H_{0}(u) & H_{1}(u) & H_{2}(u) & H_{3}(u)\\ \end{bmatrix} \begin{bmatrix} x(0) \\ x(1) \\ x'(0) \\ x'(1) \end{bmatrix}\]

\(x(0)\), \(x(1)\), \(x'(0)\), \(x'(1)\)는 \(g_{0}, g_{1}, g_{2}, g_{3}\)으로 적을 수 있으며, 가중치 역할(Control Parameter) 을 한다.

[!tip]- Basis Function와 Control Paramater의 의미{title}

\(P(u)\)는 Basis Function과 가중치 \(g_{k}\)의 결합과 같다.이다. 이 4개의 Basis Function을 잘 결합하여 모든 곡선을 만들 수 있다. \(g_{0}\)이 클수록 \(H_{0}\) 함수에 가까워지고, \(g_{1}\)이 클수록 \(H_{1}\)의 함수에 가까워지므로 \(g_{k}\)가 가중치의 역할을 한다.

[!tip]- 구현 팁{title}

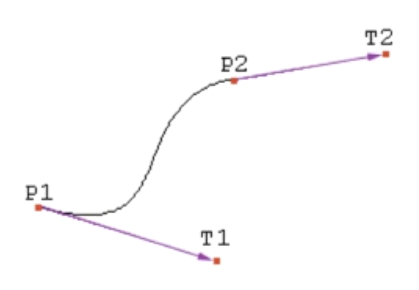
기울기를 입력받기 위해, \(T_{1}\), \(T_{2}\) 점을 추가로 생성한다. 두 점을 움직여 기울기를 조절할 수 있도록 구현하면 된다. 기울기는 \(p_{2}-T_{2}\)와 같이 계산하면 된다.

Continuity

얼마나 연결되어있는지 측정하는 지표.

1. \(C^0\) Continuity : 위치만 연속이다.
   • \(P_{1}(1) = P_{2}(0)\)
2. \(C^1\) Continuity : 위치도 같고, 기울기도 같을 때
   • \(P_{1}(1) = P_{2}(0) ~\cap~ P_{1}'(1) = P_{2}'(0)\)
3. \(C^2\) Continuity : 위치도 같고, 기울기도 같고, 가속도도 같을 때
   • \(P_{1}(1) = P_{2}(0) ~\cap~ P_{1}'(1) = P_{2}'(0) ~ \cap ~ P_{1}''(1) = P_{2}''(0)\)

애니메이션을 만들거나 게임을 만든다고 하면 제어점이 움직이는 것 까지 고려된다. 따라서 가속도가 동기화되어야 자연스러운 곡선의 움직임이 나온다.

Geometric Continuity

1. \(G^0\) Continuity : \(C^0\) Continuity와 동일함.
2. \(G^1\) Continuity : 접선 연속성. 기울기의 방향은 같지만 크기는 다를 수 있다.
   • \(P'_{1}(1) = \alpha P'_{2}(0)\)
3. \(G^2\) Continuity : 곡률 연속성.
   • \(\displaystyle \frac{\lvert P_{1}' \times P_{1}'' \rvert}{\lvert P_{1}' \rvert^3}\mid_{u=1} = \frac{\lvert P_{2}' \times P_{2}'' \rvert}{\lvert P_{2}' \rvert^3}\mid_{u=0}\)

Geometric Continuity는 말 그대로 ‘모양적으로’ 자연스러우면 될 때 사용한다. 그래픽, 산업 디자인에서 사용한다. Continuity는 애니메이션에서 사용한다.

Spline

여러개의 Curve를 연걸하여 만들어지는 하나의 매끄러운 곡선이다. 이때 곡선들이 만나는 점을 Knot라 부른다.

• Bezier Spline
  • Deg : 3
  • Continuity : \(C^0\) or \(C^1\)
  • Tangents : manual
  • Interpolation : some
  • Use Case : shapes, font & vector graphics
• Hermite Spline
  • Deg : 3
  • Continuity : \(C^0\) or \(C^1\)
  • Tangents : explicit
  • Interpolation : all
  • Use Case : animation, physics sim & interpolation
• Catnull-Rom Spline
  • Deg : 3
  • Continuity : \(C^1\)
  • Tangent : auto
  • Interpolation : all
  • Use Case : animation & path sommthing
• B-Spline
  • Deg : 3
  • Continuity : \(C^2\)
  • Tangents : auto
  • Interpolation : none
  • Use Case : curvature-sensitive shapes & animations, such as camera paths
• Linear Spline
  • Dag : 1
  • Continuity : \(C^0\)
  • Tangents : auto
  • Interpolation : all
  • Use Case : dense data & interpolation where smoothness doesn’t matter

Bezier Spline

• \(\displaystyle P(u) = \begin{cases} P_{0}(u) & 0 \leq u < 1 \\ P_{1}(u-1) & 1 \leq u < 2 \\ P_{2} (u-2) & 2 \leq u < 3 \\ \dots \end{cases}\)
  • \(P_{i}(u-i) =\) \(i\)번째 Bezier Curve

Cubic Bezier Curve를 여러개 이어서 하나의 매끄러운 곡선을 만드는 경우, Bezier Spline이다.

하나의 곡선 \(P(u)\)는 파라미터 \(u\)가 \([0, 1]\)의 범위를 갖는다. 만약 곡선을 \(n\)개 이어붙여 Spline을 만들고자 한다면, Spline 함수 \(P(u)\)의 \(u\)는 \(u\in[0,n]\)의 범위를 가지면 된다. 이후 \(u\)값을 보고, \(i\)번째 Bezier Curve를 사용해야 한다면 \(P(u) =P_{i}(u-i)\)로 위치를 계산한다.

Continuity를 만족시킬수록 사용자가 컨트롤할 수 있는 컨트롤 포인트의 수는 줄어들고, 이는 Local Control 제어권을 잃게 된다. Continuity를 덜 만족시킬 수록 Local Control 제어권이 자유로워진다. 포토샵 벡터와 같은 곳에서 Bezier Spline을 사용한다.

[!example]- Tessellation Shader로 구현한 Bazier Spline{title}

#version 400 core
#extension GL_ARB_tessellation_shader: enable

layout(isolines, equal_spacing) in;

in vec3 c2eColor[];
out vec3 e2fColor;

void main()
{
    vec4 p0 = gl_in[0].gl_Position;
    vec4 p1 = gl_in[1].gl_Position;
    vec4 p2 = gl_in[2].gl_Position;
    vec4 p3 = gl_in[3].gl_Position;

    float u = gl_TessCoord.x;
    float b0 = (1. - u) * (1. - u) * (1. - u);
    float b1 = 3. * u * (1. - u) * (1. - u);
    float b2 = 3. * u * u * (1. - u);
    float b3 = u * u * u;

    gl_Position = b0 * p0 + b1 * p1 + b2 * p2 + b3 * p3;

    // 색상 보간
    vec3 c0 = c2eColor[0];
    vec3 c1 = c2eColor[1];
    vec3 c2 = c2eColor[2];
    vec3 c3 = c2eColor[3];

    e2fColor = b0 * c0 + b1 * c1 + b2 * c2 + b3 * c3;
}

B-Spline

• Cubic B-Spline : \(\displaystyle P(u) = \sum_{i=3}^{n} P_{i}B_{i,3}(u) \implies P(u)= T_{i} M G_{i}\begin{matrix}& (\text{for }u_{i} \leq u < u_{i+1}) \end{matrix}\)
  • \(P_{i} =\) Control Point
  • \(T_{i} = \begin{bmatrix} (u-u_{i})^3 &(u - u_{i})^2 & (u-u_{i}) & 1\end{bmatrix}\)
  • \(\displaystyle M = \frac{1}{6} \begin{bmatrix}-1& 3 & -3 & 1 \\ 3 & -6 & 3&0 \\ -3 & 0 & 3 & 0 \\ 1 & 4 & 1 &0\end{bmatrix}\)
  • \(G_{i} = \begin{bmatrix} p_{i-3} \\ p_{i-2}\\ p_{i-1}\\ p_{i} \end{bmatrix}\)
• General B-Spline : \(\displaystyle P(u) = \sum_{i=d}^{n} P_{i}B_{i,d}(u)\)
  • \(n\) = Control Point의 개수
  • \(d\) = degree + 1.
  • \(\displaystyle B_{i,d}(u) = \frac{u - u_{i}}{u_{i+d-1} - u_{i}} B_{i,d-1}(u) + \frac{u_{i+d} - u}{u_{i+d} - u_{i+1}} B_{i+1,d-1}(u)\)
    • \(B_{i,1}(u) = \begin{cases} 1 & \text{if } u_{i} \leq u \leq u_{i+1} \\ 0 & \text{otherwise} \end{cases}\)
    • Basic Function 자체가 재귀적으로 정의된다.

Cubic B-Spline은 3차 다항식 곡선을 이어서 붙인 Spline과 같다. Bezier Spline과의 차이점은 (1) Basis Function이 다르고, (2) Bezier Spline의 경우 u의 Interval이 1로 고정이었지만 B-Spline은 Knot Vector를 만듦으로써 Interval를 사용자 지정할 수 있다.

Knot Vector와 모든 컨트롤 포인트 점을 Uniform 변수로 입력받으면 된다. Knot Vector를 정의하는 방법은 다음과 같다.

1. Control Point 수 + 차수 + 1 Size의 벡터를 정의한다.
2. 시작과 끝의 Knot 값을 Degree만큼 반복한다.
   1. 예를들어, 컨트롤 포인트가 6개고 Cubix B-Spline이면 \([0,0,0,1,2,3,4,4,4]\) 처럼 만든다.

앞 뒤의 Knot를 Degree만큼 반복하므로써 시작과 끝이 Control Point를 반드시 지나게 된다.

파라미터 \(u \in [u_{i}, u_{i+1})\) 범위에 영향을 미치는 Control Parameter가 \(p_{i-3}, p_{i-2}, p_{i-1}, p_{i}\)로 설정되어 있다. 그 이유는 Knot Vector와 관련있다.

매듭이 구간에 고르게 분포되면 Uniform Know Vector, 균일하지 않게 분포하면 Non-uniform Knot Vector라고 한다. ` 구현은 De Boor’s algorithm을 사용함.

NURBS

Non-uniform rational B-Spline.

• Rational B-Splines : 컨트롤 포인트에 가중치를 부여 얼마나 컨트롤 포인트에 영향을 받을거냐를 설정할 수 있다.

Catmull-Rom Spline

• \(P(u) = \left[ \begin{matrix} u^3 & u^2 & u & 1 \end{matrix} \right] \left[ \begin{matrix} -0.5 & 1.5 & -1.5 & 0.5 \\ 1 & -2.5 & 2 & -0.5 \\ -0.5 & 0 & 0.5 & 0 \\ 0 & 1 & 0 & 0 \end{matrix} \right] \left[ \begin{matrix} p_{i-1} \\ p_{i} \\ p_{i+1} \\ p_{i+2} \end{matrix} \right]\)

컨트롤 포인트 \(p_{i}, p_{i+1}\) 사이의 곡선을 보간한다. \(p_{i-1}, p_{i+2}\)는 계산에만 사용되는 Control Point이다.