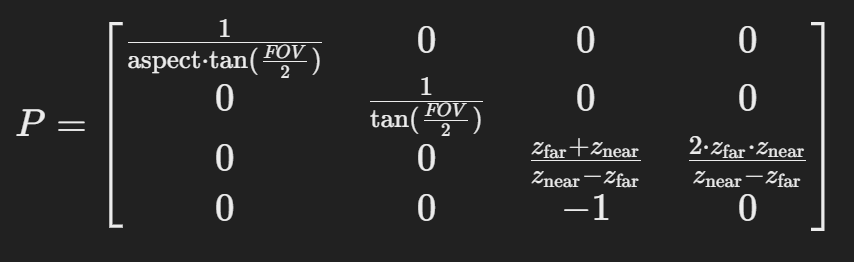고급컴퓨터그래픽스 0. Computer Graphics Review

건국대학교 고급컴퓨터그래픽스 김형석 교수님의 수업을 정리한 내용입니다.

Computer Graphics

컴퓨터를 통해 시각적인 2D, 3D 데이터를 그리는 방법을 연구하는 컴퓨터 과학의 분야이다. 우리는 3차원 그래픽스를 중점으로 다룰 것이다.

• Modeling
• Texturing
• Rendering
• Animation
• GPU Library (OpenGL, Vulkan, …)

사물의 모양을 컴퓨터로 표현하기 위해 Modeling을 이해한다. 사물의 질감, 재질, 색깔 등을 표현하기 위해 Texturing을 이해한다. 3D 정보를 2D Image로 바꾸고, 광원 그림자 효과를 구현하기 위해 Rendering을 이해한다. 사물을 시간에 따라 움직이게 하기 위해 Animation을 이해한다. 효율적인 연산을 위해 GPU Library 사용법을 이해한다.

Modeling

사물의 표면을 작은 삼각형의 모음으로 이해한다. 작은 삼각형을 잘 이어붙이면 어떤 모양이라도 만들어낼 수 있다.

Vertex는 공간 위의 한 점이다. Vertex 3개와 면의 방향(법선 벡터) 정보를 통해 하나의 삼각형을 만든다. 이를 Face라고 한다. 삼각형을 모아 하나의 모양을 만든다. 이를 Triangle Mesh라고 한다.

Texturing

색종이를 오려 붙여 표면에 덧칠하듯, Texture의 조각을 Face에 Mapping하는 방식을 사용한다.

Texture는 2D Image로 불러와 UV 좌표계로 표현된다. UV 좌표계는 \([0,1] \times [0,1]\) 정규화하여 Texture 위치를 표현한다. Vertex 하나당 UV 좌표를 하나씩 가진다.

Rendering

3차원 데이터를 가져와 화면에 대한 2차원 이미지를 생성하는 과정을 렌더링이라고 한다. 실제 우리가 보는 Screen은 2차원이기 때문에, Pipeline 과정을 거쳐 변화하게 된다. Vertex Processing, Fragment Processing은 Pipeline 과정 중 한 부분이다.

Animation

시간에 따라 Vertex의 위치를 재계산하거나, 생성하거나, 삭제하면 Animation을 구현할 수 있다.

GPU Library

QHD (2560 x 1440) 244hz 모니터는 초당 899,481,600 픽셀을 계산해야 한다. 이런 말도안되는 계산량은 끽해야 4~8코어인 CPU가 하기에는 너무 벅차므로, 이를 전문적으로 처리하는 GPU를 만들었다.

GPU는 코어를 왕창 때려박아 한번에 많은 일을 처리하는 하드웨어다. 예를들어 RTX 4070TI는 코어만 7680개가 있으며, 한 코어는 초당 23억번 (2.31GHz) 연산이 가능하다. 각 정점을 픽셀로 변환하는 작업을 몇천개의 프로세서가 병렬적으로 한번에 처리해버린다. 아무리 손이 빠른 한사람이 만두 하나 만들고, 그다음 하나 만두 만들고 해도 한세월 걸리지만, 평범한 1000명이 만두를 하나씩만 만들어도 훨씬 빨리 만들 수 있는 원리와 같다.

GPU 프로세스(코어)는 하나의 Vertex를 받으면, Graphic Pipeline or Rendering Pipeline라는 Graph 생성 단계를 폭포수처럼 쭉 거친다. 최종적으로 픽셀을 만들어, 화면에 송출한다.

Vertex Processing

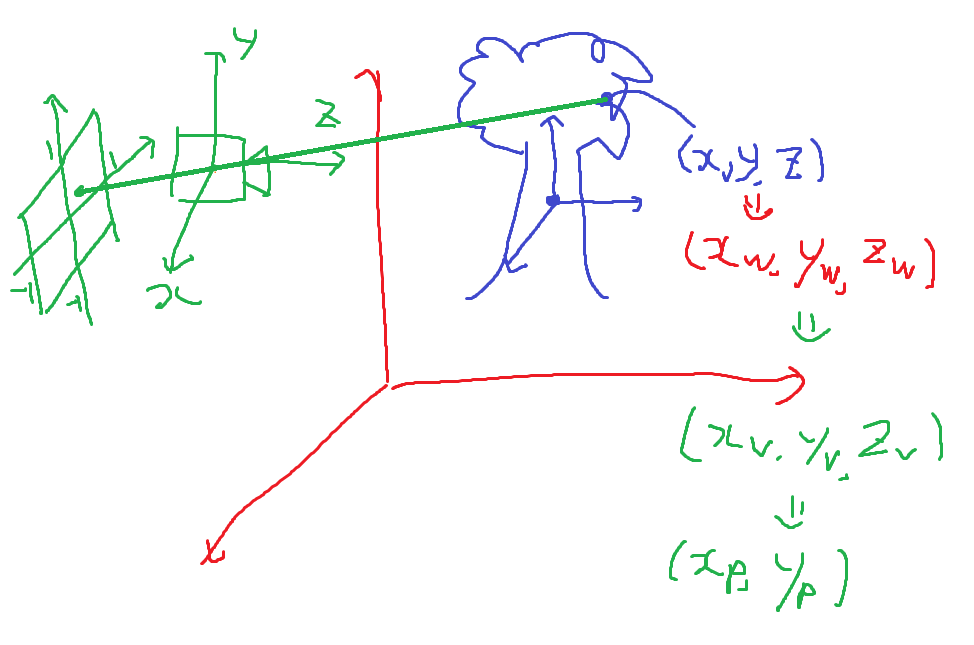
3차원 공간의 좌표를 2차원 스크린 좌표계로 옮기는 과정이다. 이를 이해하기 위해 3D 그래픽에서 사용하는 기본적인 4가지 좌표축을 이해할 필요가 있다.

1. Local Coordinate System : 모델이 갖는 원점으로부터 상대적인 위치.
2. World Coordinate System : World 기준 좌표계.
3. View (Camera) Coordinate System : Camera 기준 좌표계.
4. Normalized Coordinate System : 화면 상의 좌표계.

Normalized Coordinate System의 좌표는 \((x,y) \in [-1,1] \times [-1,1]\)에서 표현된다. 이렇게 함으로써 해상도에 의존하지 않게 된다.

입력되는 Vertex 좌표는 Local Coordinate로 표현되어있다. World Coordinate -> Camera Coordinate -> Normalized Coordinate로 좌표를 옮기면 된다. 좌표계 변환은 행렬을 사용하면 간단하다.

• Local Coordinate To World Coorinate Matrix (World Transform) = \(M_{w}\)
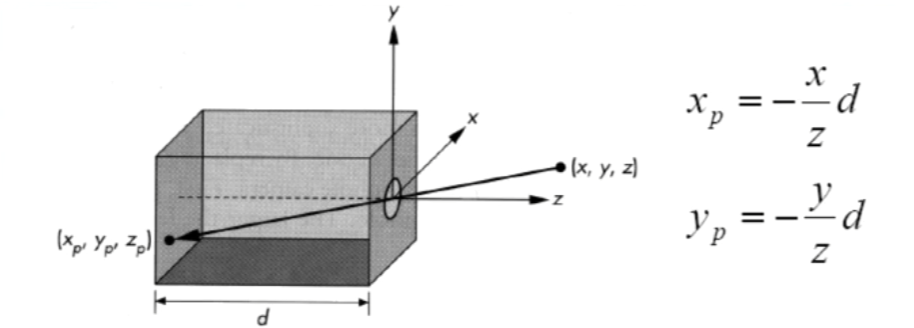
• World Coordinate To Camera Coordinate Matrix (View Transform) = \(V\)
• Camera Coordinate To Normalized Coordinate Matrix (Projection) = \(P\)

실제로 구현할땐, Model, View, Projection Matrix를 uniform 변수로 입력받아 gl_Position = PVM * vertex로 Vertex 위치를 결정하면 된다. 행렬 곱 순서가 MVP 순서대로 적용되므로, MVP 행렬이라고 불린다.

[!tip]- Model Matrix 생성 방법{title} 평행 이동을 행렬로 구현하기 위해, 차원을 하나 추가한 Homogenous Coordinate를 사용해야 한다.

• Translate Matrix : \(\displaystyle T = \begin{bmatrix} 1 & 0 & 0 & x \\ 0 & 1 & 0 & y \\ 0 & 0 & 1 & z \\ 0 & 0 & 0 & 1 \end{bmatrix}\)

• Scale Matrix : \(\displaystyle S = \begin{bmatrix}s_{x}&0&0 \\ 0&s_{y}&0 \\ 0&0&s_{z}\end{bmatrix}\)

• Rotate Matrix

  • \(\displaystyle R_x = \begin{bmatrix} 1 & 0 & 0\\ 0 & \cos\theta_x & -\sin\theta_x\\ 0 & \sin\theta_x & \cos\theta_x\end{bmatrix}\)
  • \(\displaystyle R_y = \begin{bmatrix} \cos\theta_y & 0 & \sin\theta_y \\ 0 & 1 & 0 \\ -\sin\theta_y & 0 & \cos\theta_y \end{bmatrix}\)
  • \(\displaystyle R_z = \begin{bmatrix} \cos\theta_z & -\sin\theta_z & 0 \\ \sin\theta_z & \cos\theta_z & 0 \\ 0 & 0 & 1 \end{bmatrix}​​\)

회전은 Z -> X - > Y 순서 또는 Y -> X -> Z 순서대로 많이 적용된다. \(R = R_{y} R_{x} R_{z}\)

Translate, Rotate, Scale Matrix를 생성하여, 영향을 덜 끼치는 순으로 변환하면 된다. 일반적으로, Scale -> Rotate -> Translate 순서대로 변환하는게 좋다. \(M = TRS\)

CPU에서 계산해서, shader의 uniform 변수로 넘기면 된다.

[!tip]- View Matrix 생성 방법{title}

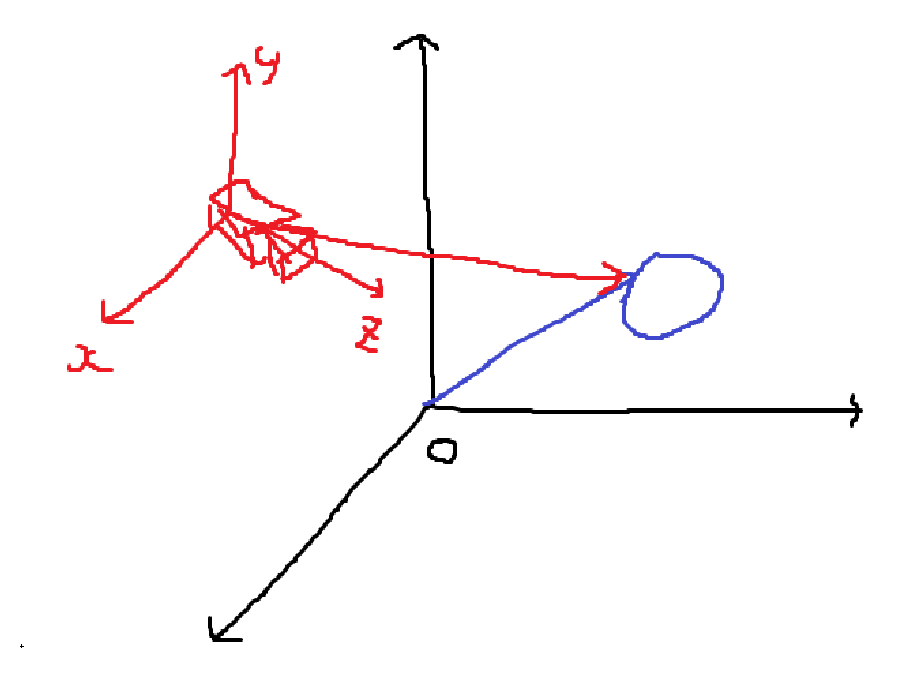
카메라를 기준으로 하는 좌표계로 Vertex를 선형 변환하는 Matrix이다.

Z축을 카메라가 보는 방향, Y축을 카메라의 위쪽 방향, X축을 카메라의 오른쪽 방향으로 지정한다. 기본적으로 정면 방향을 -Z축, 위 방향을 +Y축, Side 방향을 -X축이 가장 많이 사용하는 기본 위치다.

카메라의 Forward Vector, Up Vector는 Camera의 Field값으로 가지고 있어야 하며, 오른쪽 방향은 Forward Vector와 Up Vector를 외적하여 계산하면 된다. \(\vec{R} = \vec{F} \times \vec{U}\)

Camera의 Basis Vector를 계산한 후, 좌표계 변환을 해야한다.

Camera Position을 사용하여 Camera Coordinate를 원점으로 옮기고, 선형 변환의 역행렬을 사용해 좌표계 변환 행렬을 적용하면 된다.

\(T_{x}, T_{y}, T_{z}\) = Camera Position

\[V = \begin{bmatrix}R_{x}&U_{x} & F_{x}& 0 \\ R_{y}&U_{y} & F_{y} & 0 \\R_{z} & U_{z} & F_{z} & 0 \\ 0 & 0 & 0 & 1\end{bmatrix}^T \cdot \begin{bmatrix}1&0 & 0& - T_{x} \\ 0&1 & 0 & - T_{y} \\0 & 0 &1 & -T_{z} \\ 0 & 0 & 0 & 1\end{bmatrix}\] \[= \begin{bmatrix}R_{x}&R_{y} & R_{z}& 0\\ U_{x}&U_{y} & U_{z} & 0 \\ F_{x} & F_{y} & F_{z} & 0 \\ 0 & 0 & 0 & 1\end{bmatrix} \cdot \begin{bmatrix}1&0 & 0& - T_{x} \\ 0&1 & 0 & - T_{y} \\0 & 0 &1 & -T_{z} \\ 0 & 0 & 0 & 1\end{bmatrix}\]

[!tip]- Projection Matrix 생성 방법{title}

Fragment Processing

광원, 재질, 텍스쳐 등을 고려하여 최종적인 Fragment의 Color를 결정하는 단계다.